题目内容
已知圆的方程为(x-t)2+(y-t-1)2=2(t∈[-2,2]),则它的圆心的轨迹方程为( )
| A、x-y+1=0,x∈[-2,2] |
| B、x+y+1=0,x∈[-2,2] |
| C、x-y-1=0,x∈[-2,2] |
| D、x+y-1=0,x∈[-2,2] |
考点:圆的一般方程,轨迹方程
专题:计算题,直线与圆
分析:求出圆心坐标,消参可得结论.
解答:
解:设圆心为(x,y),则x=t,y=t+1(t∈[-2,2]),
所以y=x+1,x∈[-2,2],
故选:A.
所以y=x+1,x∈[-2,2],
故选:A.
点评:本题考查圆的方程,考查轨迹方程,确定圆心坐标是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
平行四边形ABCD中,∠CBA=120°,AD=4,对角线BD=2
,将其沿对角线BD折起,使平面ABD⊥平面BCD,若四面体ABCD顶点在同一个球面上,则该球的体积为( )
| 3 |
A、
| ||||
B、
| ||||
C、32
| ||||
| D、2π |
过点(2,
)且平行于极轴的直线的坐标方程为( )
| π |
| 3 |
A、ρsinθ=
| ||
B、ρcosθ=
| ||
| C、ρsinθ=2 | ||
| D、ρcosθ=2 |
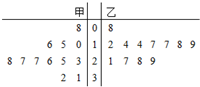 如图是某篮球联赛中,甲、乙两名运动员12个场次得分的茎叶图.设甲、乙两人得分的平均数分别为
如图是某篮球联赛中,甲、乙两名运动员12个场次得分的茎叶图.设甲、乙两人得分的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|