题目内容
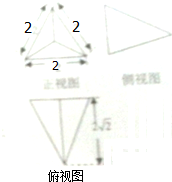
已知三棱锥的三视图,则该三棱锥的体积是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:如图所示,AB=BC=CA=2,点P在侧面ABC的射影为O,OP=2
.利用三棱锥的体积计算公式即可得出.
| 2 |
解答:
解:如图所示, AB=BC=CA=2,点P在侧面ABC的射影为O,OP=2
AB=BC=CA=2,点P在侧面ABC的射影为O,OP=2
.
∴该三棱锥的体积V=
•S△ABC•OP=
×
×22×2
=
.
故选:B.
 AB=BC=CA=2,点P在侧面ABC的射影为O,OP=2
AB=BC=CA=2,点P在侧面ABC的射影为O,OP=2| 2 |
∴该三棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 2 |
2
| ||
| 3 |
故选:B.
点评:本题考查了三棱锥的三视图及其体积计算公式,属于基础题.

练习册系列答案
相关题目
平行四边形ABCD中,∠CBA=120°,AD=4,对角线BD=2
,将其沿对角线BD折起,使平面ABD⊥平面BCD,若四面体ABCD顶点在同一个球面上,则该球的体积为( )
| 3 |
A、
| ||||
B、
| ||||
C、32
| ||||
| D、2π |
过点(2,
)且平行于极轴的直线的坐标方程为( )
| π |
| 3 |
A、ρsinθ=
| ||
B、ρcosθ=
| ||
| C、ρsinθ=2 | ||
| D、ρcosθ=2 |
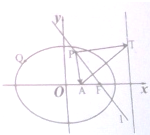 如图,Q为椭圆E:
如图,Q为椭圆E: