题目内容
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
（1）求函数f（x）的表达式；
（2）把f（x）的图象向右平移
| π |
| 4 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换
专题：综合题,三角函数的图像与性质
分析：（1）根据周期确定ω，将y=Asin2x的图象向左平移
，得y=Asin（2x+φ）的图象，可求φ，代入（0，1），可求A，从而可求函数f（x）的表达式；
（2）确定把f（x）的图象向右平移
个单位长度得到g（x）的图象，再求g（x）的对称轴方程和对称中心．
| π |
| 12 |
（2）确定把f（x）的图象向右平移
| π |
| 4 |
解答：
解：（1）由图知，T=π，于是ω=
=2．…（2分）
将y=Asin2x的图象向左平移
，得y=Asin（2x+φ）的图象，于是φ=2×
=
．
将（0，1）代入y=Asin（2x+
），得A=2．
故f（x）=2sin（2x+
）． …（6分）
（2）依题意，g（x）=2sin[2（x-
）+
]=-2cos（2x+
），…（8分）
求对称轴：令2x+
=kπ（k∈Z），则x=
-
（k∈z）
∴g（x）的对称轴为：x=
-
（k∈z）…（10分）
求对称中心：令2x+
=kπ+
（k∈Z），则x=
+
（k∈z）
∴g（x）的对称中心为：(
+
，0)（k∈z）…（12分）
| 2π |
| T |
将y=Asin2x的图象向左平移
| π |
| 12 |
| π |
| 12 |
| π |
| 6 |
将（0，1）代入y=Asin（2x+
| π |
| 6 |
故f（x）=2sin（2x+
| π |
| 6 |
（2）依题意，g（x）=2sin[2（x-
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
求对称轴：令2x+
| π |
| 6 |
| kπ |
| 2 |
| π |
| 12 |
∴g（x）的对称轴为：x=
| kπ |
| 2 |
| π |
| 12 |
求对称中心：令2x+
| π |
| 6 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 6 |
∴g（x）的对称中心为：(
| kπ |
| 2 |
| π |
| 6 |
点评：本题考查函数y=Asin（ωx+φ）的解析式、图象变换，着重考查正弦函数的对称中心的应用，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
如图所示是某一几何体的三视图，则它的体积为（ ）
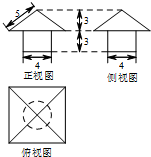
| A、16+12π |
| B、48+12π |
| C、64+12π |
| D、64+16π |
若曲线y=x2+ax+b在点（1，b）处的切线方程是x-y+1=0，则（ ）
| A、a=1，b=2 |
| B、a=-1，b=2 |
| C、a=1，b=-2 |
| D、a=-1，b=-2 |
下列命题中的真命题是（ ）
| A、?x∈R，x2＞0 | ||
B、?x∈R，x+
| ||
| C、?x0∈R，sinx0+cosx0=2 | ||
D、?x0∈R，ln x0＞（
|
圆C：（x+1）2+（y-3）2=9上有两点P，Q关于直线x+my+4=0对称，则m等于（ ）
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
2013年4月20日8点02分四川省雅安市芦山县（北纬30.3度，东经103.0度）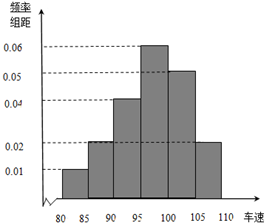
2013年国庆期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段[80，85），[85，90），[90，95），[95，100），[100，105），[105，110）后得到如下图的频率分布直方图．
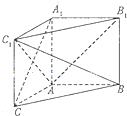如图，在直三棱柱ABC-A1B1C1中，AB⊥AC，且AB=AC=AA1=1．