题目内容
已知椭圆C:
+
=1(a>b>0)短轴的两个顶点与右焦点的连线构成等边三角形,直线3x+4y+6=0与以椭圆C的上顶点为圆心,以椭圆C的长半轴长为半径的圆相切.
(1)求椭圆C的方程;
(2)椭圆C与x轴负半轴交于点A,过点A的直线AM、AN分别与椭圆C交于M、N两点,kAM、kAN分别为直线AM、AN的斜率,kAM•kAN=-
,求证:直线MN过定点,并求出该定点坐标;
(3)在(2)的条件下,求△AMN面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的方程;
(2)椭圆C与x轴负半轴交于点A,过点A的直线AM、AN分别与椭圆C交于M、N两点,kAM、kAN分别为直线AM、AN的斜率,kAM•kAN=-
| 3 |
| 4 |
(3)在(2)的条件下,求△AMN面积的最大值.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:计算题,证明题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)由等边三角形,得到a=2b,再由直线和圆相切的条件,得到5a=4b+6,解得a,b,即可得到椭圆方程;
(2)设出直线MN的方程,和M,N的坐标,把直线方程与椭圆方程联立,利用韦达定理表示出x1+x2和x1x2,进而利用kAM•kAN=-
,求得k,t的关系,进而可求得直线MN恒过定点;
(3)设直线MN:x=my-1,联立椭圆方程,消去x,运用韦达定理,再由△AMN面积为S=
|AQ|•|y1-y2|,代入化简整理,再由对勾函数的性质,即可得到最大值.
(2)设出直线MN的方程,和M,N的坐标,把直线方程与椭圆方程联立,利用韦达定理表示出x1+x2和x1x2,进而利用kAM•kAN=-
| 3 |
| 4 |
(3)设直线MN:x=my-1,联立椭圆方程,消去x,运用韦达定理,再由△AMN面积为S=
| 1 |
| 2 |
解答:
(1)解:由于短轴的顶点与右焦点的距离为a,
则由短轴的两个顶点与右焦点的连线构成等边三角形,则a=2b,
又直线3x+4y+6=0与以椭圆C的上顶点为圆心,以椭圆C的长半轴长为半径的圆相切,
则d=
=a,即有5a=4b+6,
解得,a=2,b=1.
则椭圆方程为:
+y2=1;
(2)证明:设直线MN的方程为y=kx+t,M、N坐标分别为M(x1,y1)、N(x2,y2),
由
⇒(1+4k2)x2+8ktx+4t2-4=0.
判别式为64k2t2-4(1+4k2)(4t2-4)>0,
∴x1+x2=-
,x1x2=
,
∵kAM=
,kAN=
,
∴kAM•kAN=
=
=-
,
将韦达定理代入,并整理得
=-
,化简得,t2-3kt+2k2=0,
即有t=k或t=2k,则直线MN的方程为y=k(x+1)或y=k(x+2),
由于A(-2,0),则直线MN恒过定点Q(-1,0);
(3)解:△AMN面积为S=
|AQ|•|y1-y2|,
设直线MN:x=my-1,联立椭圆方程,得到(4+m2)y2-2my-3=0,
则y1+y2=
,y1y2=
,
则S=
=
=
=
令
=u(u≥
),则u+
在[
,+∞)递增,当u=
,即有m=0,
则u+
取最小值
,此时S取得最大值2×
=
.
则由短轴的两个顶点与右焦点的连线构成等边三角形,则a=2b,
又直线3x+4y+6=0与以椭圆C的上顶点为圆心,以椭圆C的长半轴长为半径的圆相切,
则d=
| |0+4b+6| | ||
|
解得,a=2,b=1.
则椭圆方程为:
| x2 |
| 4 |
(2)证明:设直线MN的方程为y=kx+t,M、N坐标分别为M(x1,y1)、N(x2,y2),
由
|
判别式为64k2t2-4(1+4k2)(4t2-4)>0,
∴x1+x2=-
| 8kt |
| 1+4k2 |
| 4t2-4 |
| 1+4k2 |
∵kAM=
| y1 |
| x1+2 |
| y2 |
| x2+2 |
∴kAM•kAN=
| (kx1+t)(kx2+t) |
| (x1+2)(x2+2) |
| k2x1x2+kt(x1+x2)+t2 |
| x1x2+2(x1+x2)+4 |
| 3 |
| 4 |
将韦达定理代入,并整理得
| t2-4k2 |
| 4t2-16kt+16k2 |
| 3 |
| 4 |
即有t=k或t=2k,则直线MN的方程为y=k(x+1)或y=k(x+2),
由于A(-2,0),则直线MN恒过定点Q(-1,0);
(3)解:△AMN面积为S=
| 1 |
| 2 |
设直线MN:x=my-1,联立椭圆方程,得到(4+m2)y2-2my-3=0,
则y1+y2=
| 2m |
| 4+m2 |
| -3 |
| 4+m2 |
则S=
| 1 |
| 2 |
| (y1+y2)2-4y1y2 |
| 1 |
| 2 |
(
|
2
| ||
| 4+m2 |
| 2 | ||||||
|
令
| 3+m2 |
| 3 |
| 1 |
| u |
| 3 |
| 3 |
则u+
| 1 |
| u |
4
| ||
| 3 |
| 3 | ||
4
|
| ||
| 2 |
点评:本题考查椭圆的方程和性质,考查直线和圆相切的条件,考查联立直线方程和椭圆方程,消去未知数,运用韦达定理,以及化简整理的运算能力,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
若l,m表示直线,α,β,γ表示平面,则下列命题不正确的是( )
| A、若l⊥m,l⊥α,m⊥β,则α⊥β |
| B、若l⊥m,l?α,m?β,则α⊥β |
| C、若α⊥γ,β∥γ,则α⊥β |
| D、若l∥m,l⊥α,m?β,则α⊥β |
双曲线y=
的焦距为( )
| 1 |
| x |
A、
| ||
B、2
| ||
| C、2 | ||
| D、4 |
将形如M=mn(m、n∈N*)的正整数表示成各项都是整数、公差为2的等差数列的前m项和,称作“对M的m项分划”.例如,将4表示成4=22=1+3,称作“对4的2项分划”,将27表示成27=33=7+9+11,称作“对27的3项分划”.那么对256的16项分划中,最大的数是( )( )
| A、19 | B、21 | C、31 | D、39 |
方程2sin2x=x-3的解有( )个.
| A、1 | B、2 | C、3 | D、4 |
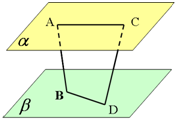 已知AB、CD是夹在平行平面α、β间的异面线段,A,C∈α,B,D∈β,且AC=6,BD=8,AB=CD=10,AB和CD成60°角.求异面直线AC和BD所成的角.
已知AB、CD是夹在平行平面α、β间的异面线段,A,C∈α,B,D∈β,且AC=6,BD=8,AB=CD=10,AB和CD成60°角.求异面直线AC和BD所成的角.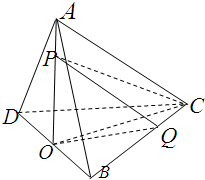 如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为
如图,在三棱锥A-BCD中,BC=DC=AB=AD=2,BD=2,平面ABD⊥平面BCD,O为BD中点,点P,Q分别为线段AO,BC上的动点(不含端点),且AP=CQ,则三棱锥P-QCO体积的最大值为