题目内容
已知等比数列{an}的首项a1=
,前n项和为Sn,满足s1、2s2、3s3成等差数列;
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=2-(
+
)),数列bn的前n项和为Tn,求证:Tn<
.
| 1 |
| 3 |
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=2-(
| 1 |
| 1+an |
| 1 |
| 1-an+1 |
| 1 |
| 3 |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知得4•
=a1+3•
,由此求出an=(
)n.
(Ⅱ)bn=2-(
+
)=2-(
+
)=
-
,从而bn<
-
,由此能证明Tn<
.
| a1(1-q2) |
| 1-q |
| a1(1-q3) |
| 1-q |
| 1 |
| 3 |
(Ⅱ)bn=2-(
| 1 |
| 1+an |
| 1 |
| 1-an+1 |
| 1 | ||
1+(
|
| 1 | ||
1-(
|
| 1 |
| 3n+1 |
| 1 |
| 3n+1-1 |
| 1 |
| 3n |
| 1 |
| 3n+1 |
| 1 |
| 3 |
解答:
(Ⅰ)解:∵S1、2S2、3S3成等差数列,
∴4S2=S1+3S3,
当q=1时,不符合,
当q≠1时,得4•
=a1+3•
,
由a1=
,解得q=
或q=0(舍),
∴an=(
)n.
(Ⅱ)证明:bn=2-(
+
)=2-(
+
)
=2-
-
=1-
+1-
=(1-
)+(1-
)
=
-
,
由
<
,
>
,得
<
-
,
∴bn<
-
,
从而Tn<(
-
)+(
-
)+…+(
-
)=
-
<
,
∴Tn<
.
∴4S2=S1+3S3,
当q=1时,不符合,
当q≠1时,得4•
| a1(1-q2) |
| 1-q |
| a1(1-q3) |
| 1-q |
由a1=
| 1 |
| 3 |
| 1 |
| 3 |
∴an=(
| 1 |
| 3 |
(Ⅱ)证明:bn=2-(
| 1 |
| 1+an |
| 1 |
| 1-an+1 |
| 1 | ||
1+(
|
| 1 | ||
1-(
|
=2-
| 1 | ||
1+(
|
| 1 | ||
1-(
|
=1-
| 1 | ||
1+(
|
| 1 | ||
1-(
|
=(1-
| 3n |
| 3n+1 |
| 3n+1 |
| 3n+1-1 |
=
| 1 |
| 3n+1 |
| 1 |
| 3n+1-1 |
由
| 1 |
| 3n+1 |
| 1 |
| 3n |
| 1 |
| 3n+1-1 |
| 1 |
| 3n+1 |
| 1 |
| 3n+1-1 |
| 1 |
| 3n |
| 1 |
| 3n+1 |
∴bn<
| 1 |
| 3n |
| 1 |
| 3n+1 |
从而Tn<(
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
| 1 |
| 3n+1 |
| 1 |
| 3 |
| 1 |
| 3n+1 |
| 1 |
| 3 |
∴Tn<
| 1 |
| 3 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,是中档题,解题时要注意裂项求和法的合理运用.

练习册系列答案
相关题目
已知α,β是平面,a,b,c是直线,O是点.下列五个命题:
①若α∥β,a?α,b?β,则a∥b;
②若a∥b,a⊥c,则b⊥c;
③若a∥α,b?α,则a∥b;
④若a∥α,b∥α,则a∥b;
⑤若a∩b=O,a∥α,则b与α平行或相交.
其中正确的有( )
①若α∥β,a?α,b?β,则a∥b;
②若a∥b,a⊥c,则b⊥c;
③若a∥α,b?α,则a∥b;
④若a∥α,b∥α,则a∥b;
⑤若a∩b=O,a∥α,则b与α平行或相交.
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
方程2sin2x=x-3的解有( )个.
| A、1 | B、2 | C、3 | D、4 |
下列说法错误的是( )
| A、在统计里,从总体中抽取的一部分个体叫做总体的一个样本,样本中个体的数目叫做样本的容量 |
| B、一组数据的平均数一定大于这组数据中的每个数据 |
| C、平均数、众数与中位数从不同的角度描述了一组数据的集中趋势 |
| D、一组数据的方差越大,说明这组数据的波动性越大 |
曲线
+
=1与曲线
+
=1(m<3)的( )
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4-m |
| y2 |
| 3-m |
| A、长轴长相等 | B、短轴长相等 |
| C、离心率相等 | D、焦距相等 |
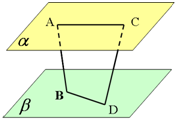 已知AB、CD是夹在平行平面α、β间的异面线段,A,C∈α,B,D∈β,且AC=6,BD=8,AB=CD=10,AB和CD成60°角.求异面直线AC和BD所成的角.
已知AB、CD是夹在平行平面α、β间的异面线段,A,C∈α,B,D∈β,且AC=6,BD=8,AB=CD=10,AB和CD成60°角.求异面直线AC和BD所成的角.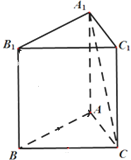 在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10.求证:
在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AB=8,AC=6,BC=10.求证: