题目内容
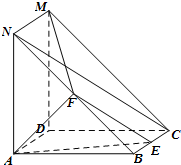 如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.
如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.(Ⅰ)当E为线段BC中点时,求证:NC∥平面AEF;
(Ⅱ)求证:平面AEF⊥BCMN平面;
(Ⅲ)设
| BE |
| BC |
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件推导出NC∥EF,由此能证明NC∥平面AEF.
(Ⅱ)由已知条件推导出AD⊥平面NAB,从而得到AD⊥AF,BC⊥AF,再由AF⊥NB,推导出AF⊥平面BCMN,由此能证明平面AEF⊥平面BCMN.
(Ⅲ)利用直线与平面垂直的判定定理,结合题设条件得到λ=
时,MF⊥平面AEF.
(Ⅱ)由已知条件推导出AD⊥平面NAB,从而得到AD⊥AF,BC⊥AF,再由AF⊥NB,推导出AF⊥平面BCMN,由此能证明平面AEF⊥平面BCMN.
(Ⅲ)利用直线与平面垂直的判定定理,结合题设条件得到λ=
| 1 |
| 2 |
解答:
(Ⅰ)证明:∵F为线段NB的中点,E为线段BC中点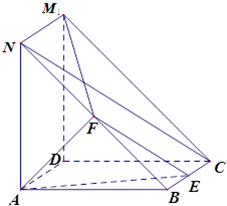 ,
,
∴NC∥EF,又NC不包含平面AEF,EF?平面AEF,
∴NC∥平面AEF.(4分)
(Ⅱ)证明:四边形ABCD与四边形ADMN都为正方形,
∴AD⊥NA,AD⊥AB,
NA∩AB=A,∴AD⊥平面NAB,
AF?平面NAB,故AD⊥AF,
AD∥BC,∴BC⊥AF,
由题意NA=AB,F为线段NB的中点,
∴AF⊥NB,
NB∩BC=B,∴AF⊥平面BCMN,
∵AF?平面AEF,
∴平面AEF⊥平面BCMN.(11分)
(Ⅲ)解:λ=
时,MF⊥平面AEF.(14分)
 ,
,∴NC∥EF,又NC不包含平面AEF,EF?平面AEF,
∴NC∥平面AEF.(4分)
(Ⅱ)证明:四边形ABCD与四边形ADMN都为正方形,
∴AD⊥NA,AD⊥AB,
NA∩AB=A,∴AD⊥平面NAB,
AF?平面NAB,故AD⊥AF,
AD∥BC,∴BC⊥AF,
由题意NA=AB,F为线段NB的中点,
∴AF⊥NB,
NB∩BC=B,∴AF⊥平面BCMN,
∵AF?平面AEF,
∴平面AEF⊥平面BCMN.(11分)
(Ⅲ)解:λ=
| 1 |
| 2 |
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,考查满足条件的实数值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
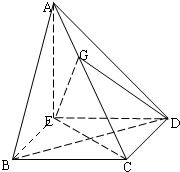 如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6
如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6 已知某几何体的三视图如图所示,其中正视图与侧视图都是直角边为2的等腰直角三角形,则该几何体的表面积为
已知某几何体的三视图如图所示,其中正视图与侧视图都是直角边为2的等腰直角三角形,则该几何体的表面积为