题目内容
在平面直角坐标系xOy中,椭圆C:
+
=1(a>b>0)的上顶点到焦点的距离为2,离心率为
.
(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题设知a=2,e=
=
,由此能求出a=2,b=1.
(2)(i)由(1)得,椭圆C的方程为
+y2=1.设点P(m,0)(-2≤m≤2),点A(x1,y1),点B(x2,y2).若k=1,则直线l的方程为y=x-m.联立直线l与椭圆C的方程,得
x2-2mx+m2-1=0.|AB|=
•
,点O到直线l的距离d=
,由此求出S△OAB取得最大值1.
(ⅱ)设直线l的方程为y=k(x-m).将直线l与椭圆方程联立,得(1+4k2)x2-8mk2x+4(k2m2-1)=0,由此利用韦达定理结合已知条件能求出k的.
| c |
| a |
| ||
| 2 |
(2)(i)由(1)得,椭圆C的方程为
| x2 |
| 4 |
| 5 |
| 4 |
| 4 |
| 5 |
| 2 |
| 5-m2 |
| |m| | ||
|
(ⅱ)设直线l的方程为y=k(x-m).将直线l与椭圆方程联立,得(1+4k2)x2-8mk2x+4(k2m2-1)=0,由此利用韦达定理结合已知条件能求出k的.
解答:
(本小题满分16分)
解:(1)由题设知a=2,e=
=
,
所以c=
,故b2=4-3=1.
因此,a=2,b=1.…(2分)
(2)(i)由(1)可得,椭圆C的方程为
+y2=1.
设点P(m,0)(-2≤m≤2),点A(x1,y1),点B(x2,y2).
若k=1,则直线l的方程为y=x-m.
联立直线l与椭圆C的方程,
即
.将y消去,化简得
x2-2mx+m2-1=0.
解得x1=
,x2=
,
从而有,x1+x2=
,x1•x2=
,
而y1=x1-m,y2=x2-m,
因此,|AB|=
=
=
•
=
•
,
点O到直线l的距离d=
,
所以,S△OAB=
×|AB|×d=
×|m|,
因此,S2△OAB=
( 5-m2)×m2≤
•(
)2=1.…(6分)
又-2≤m≤2,即m2∈[0,4].
所以,当5-m2=m2,即m2=
,m=±
时,S△OAB取得最大值1.…(8分)
(ⅱ)设直线l的方程为y=k(x-m).
将直线l与椭圆C的方程联立,即
.
将y消去,化简得(1+4k2)x2-8mk2x+4(k2m2-1)=0,
解得,x1+x2=
,x1•x2=
.…(10分)
所以PA2+PB2=(x1-m)2+y12+(x2-m)2+y22
=
(x12+x22)-2m(x1+x2)+2m2+2
=
(*).…(14分)
因为PA2+PB2的值与点P的位置无关,即(*)式取值与m无关,
所以有-8k4-6k2+2=0,解得k=±
.
所以,k的值为±
.…(16分)
解:(1)由题设知a=2,e=
| c |
| a |
| ||
| 2 |
所以c=
| 3 |
因此,a=2,b=1.…(2分)
(2)(i)由(1)可得,椭圆C的方程为
| x2 |
| 4 |
设点P(m,0)(-2≤m≤2),点A(x1,y1),点B(x2,y2).
若k=1,则直线l的方程为y=x-m.
联立直线l与椭圆C的方程,
即
|
| 5 |
| 4 |
解得x1=
2(2m-
| ||
| 5 |
2(2m+
| ||
| 5 |
从而有,x1+x2=
| 8m |
| 5 |
| 4(m2-1) |
| 5 |
而y1=x1-m,y2=x2-m,
因此,|AB|=
| (x1-x2)2+(y1-y2)2 |
| 2(x1-x2)2 |
| 2 |
| (x1+x2)2-4x1x2 |
=
| 4 |
| 5 |
| 2 |
| 5-m2 |
点O到直线l的距离d=
| |m| | ||
|
所以,S△OAB=
| 1 |
| 2 |
| 2 |
| 5 |
| 5-m2 |
因此,S2△OAB=
| 4 |
| 25 |
| 4 |
| 25 |
| 5-m2+m2 |
| 2 |
又-2≤m≤2,即m2∈[0,4].
所以,当5-m2=m2,即m2=
| 5 |
| 2 |
| ||
| 2 |
(ⅱ)设直线l的方程为y=k(x-m).
将直线l与椭圆C的方程联立,即
|
将y消去,化简得(1+4k2)x2-8mk2x+4(k2m2-1)=0,
解得,x1+x2=
| 8mk2 |
| 1+4k2 |
| 4(k2m2-1) |
| 1+4k2 |
所以PA2+PB2=(x1-m)2+y12+(x2-m)2+y22
=
| 3 |
| 4 |
=
| m2(-8k4-6k2+2)+(1+4k2)(8k2+8) |
| (1+4k2)2 |
因为PA2+PB2的值与点P的位置无关,即(*)式取值与m无关,
所以有-8k4-6k2+2=0,解得k=±
| 1 |
| 2 |
所以,k的值为±
| 1 |
| 2 |
点评:本题考查椭圆方程中的参数的求法,考查三角形面积的最大值的求法,考查直线的斜率的求法,解题时要认真审题,注意椭圆弦长公式的合理运用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
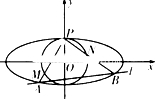 如图,椭圆C:
如图,椭圆C: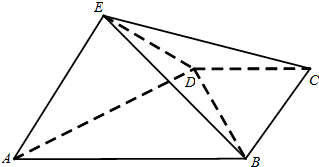 如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.
如图,四棱锥E-ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2.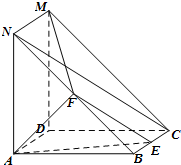 如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.
如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.