题目内容
过点P（3，0）作一直线l，使它被两直线l1：2x-y-2=0和l2：x+y+3=0所截的线段AB以P为中点，求此直线l的方程．
考点：待定系数法求直线方程
专题：直线与圆
分析：（1）当k不存在时，不满足题意；（2）当k存在时，设直线l：y=k（x-3），分别联立方程组可得A、B坐标，由中点公式可得k的方程，解之可得所求．
解答：
解：（1）当斜率k不存在时，可得直线的方程l：x=3，不满足题意；
（2）当斜率k存在时，设直线l：y=k（x-3），
联立方程组可得
，解方程组可得A(
，
)，
同理联立方程组
，解方程组可得B(
，
)，…（6分）
由中点坐标公式得
+
=6，解得k=8，
∴直线l方程为y=8x-24，化为一般式8x-y-24=0
（2）当斜率k存在时，设直线l：y=k（x-3），
联立方程组可得
|
| 2-3k |
| 2-k |
| -4k |
| 2-k |
同理联立方程组
|
| 3k-3 |
| k+1 |
| -6k |
| k+1 |
由中点坐标公式得
| 2-3k |
| 2-k |
| 3k-3 |
| k+1 |
∴直线l方程为y=8x-24，化为一般式8x-y-24=0
点评：本题考查直线的一般式方程，涉及待定系数法求直线的方程和中点公式，属基础题．
练习册系列答案
相关题目
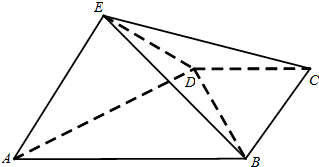如图，四棱锥E-ABCD中，平面EAD⊥平面ABCD，DC∥AB，BC⊥CD，EA⊥ED，且AB=4，BC=CD=EA=ED=2．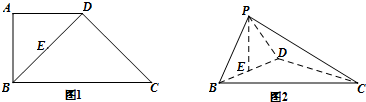
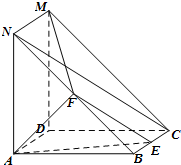如图，四边形ABCD与四边形ADMN都为正方形，AN⊥AB，F为线段BN的中点，E为线段BC上的动点．