题目内容
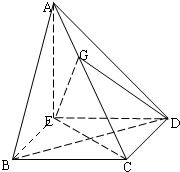 如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6
如图,在四棱锥A-BCDE中,AE⊥平面BCDE,∠ABC=∠BCD=∠CDA=90°,AC=6| 3 |
(Ⅰ)求证:BD⊥平面ACE;
(Ⅱ)设点G在棱AC上,且CG=2GA,试求三棱锥E-GCD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明BD⊥平面ACE,只需证明AE⊥BD,BD⊥CE;
(Ⅱ)过G作GH∥AE交EC于H,证明GH⊥平面DEC,即可求三棱锥E-GCD的体积.
(Ⅱ)过G作GH∥AE交EC于H,证明GH⊥平面DEC,即可求三棱锥E-GCD的体积.
解答:
 (I)证明:由AE⊥平面BCDE得AE⊥BD,
(I)证明:由AE⊥平面BCDE得AE⊥BD,
又∠ABC=∠BCD=∠CDA=90°,
∴∠EBC=∠BCD=∠CDE=90°,
∴四边形BCDE为平行四边形,
∵BC=CD,∴四边形BCDE为正方形,
∴BD⊥CE
又AE?平面ACE,CE?平面ACE,AE∩CE=E
故BD⊥平面ACE,…6分
(Ⅱ)解:过G作GH∥AE交EC于H,…7分
∵CG=2GA,∴GH=
AE,
∵AE⊥平面BCDE,∴GH⊥平面DEC,AE⊥EC…9分
在直角三角形AEC中,CE=6
,AC=6
,得AE=6,∴GH=
AE=4
∴三棱锥E-GCD的体积VG-ECD=
×
×6×6×4=24…12分.
 (I)证明:由AE⊥平面BCDE得AE⊥BD,
(I)证明:由AE⊥平面BCDE得AE⊥BD,又∠ABC=∠BCD=∠CDA=90°,
∴∠EBC=∠BCD=∠CDE=90°,
∴四边形BCDE为平行四边形,
∵BC=CD,∴四边形BCDE为正方形,
∴BD⊥CE
又AE?平面ACE,CE?平面ACE,AE∩CE=E
故BD⊥平面ACE,…6分
(Ⅱ)解:过G作GH∥AE交EC于H,…7分
∵CG=2GA,∴GH=
| 2 |
| 3 |
∵AE⊥平面BCDE,∴GH⊥平面DEC,AE⊥EC…9分
在直角三角形AEC中,CE=6
| 2 |
| 3 |
| 2 |
| 3 |
∴三棱锥E-GCD的体积VG-ECD=
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题考查直线与平面垂直的判定,考查三棱锥E-GCD的体积,正确运用直线与平面垂直的判定定理是关键.

练习册系列答案
相关题目
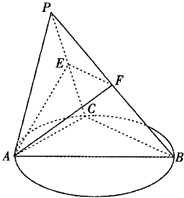 如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F 分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F 分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.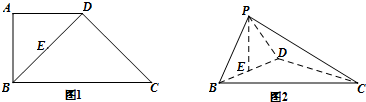
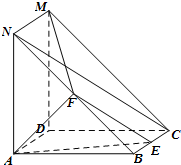 如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.
如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.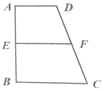 如图梯形ABCD中,AD∥BC,∠ABC=90°,AD:BC:AB=2:3:4,E、F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论:
如图梯形ABCD中,AD∥BC,∠ABC=90°,AD:BC:AB=2:3:4,E、F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论: