题目内容
已知直线l1:x+y-3=0与直线l2:x-3y+1=0相交于点C,以C为圆心的圆过点A(0,1).
(1)求圆C的方程;
(2)求过点B(4,5)的圆C的切线方程.
(1)求圆C的方程;
(2)求过点B(4,5)的圆C的切线方程.
考点:圆的切线方程,圆的标准方程
专题:综合题,直线与圆
分析:(1)求出交点,可得C的坐标,求出半径,可得圆C的方程;
(2)分情况讨论,切线斜率存在和不存在两种,当切线斜率存在时,设切线l的方程为:y-5=k(x-4)化为一般式,利用圆心到直线的距离等于半径运算即可;②当切线斜率不存在时,直接检验即可.
(2)分情况讨论,切线斜率存在和不存在两种,当切线斜率存在时,设切线l的方程为:y-5=k(x-4)化为一般式,利用圆心到直线的距离等于半径运算即可;②当切线斜率不存在时,直接检验即可.
解答:
解:(1)由直线l1:x+y-3=0与直线l2:x-3y+1=0相交于点C,可得C(2,1),
∵以C为圆心的圆过点A(0,1),
∴圆的半径为2,
∴圆的方程为(x-2)2+(y-1)2=4;
(2)①当切线斜率存在时,设切线l的方程为:y-5=k(x-4)
即:kx-y+5-4k=0
由
=2得k=
,
∴切线方程l:3x-4y+8=0
②当切线斜率不存在时,过点P(4,5)的直线为x=4
经检验是圆(x-2)2+(y-1)2=4的切线.
∴切线方程为3x-4y+8=0或x=4.
∵以C为圆心的圆过点A(0,1),
∴圆的半径为2,
∴圆的方程为(x-2)2+(y-1)2=4;
(2)①当切线斜率存在时,设切线l的方程为:y-5=k(x-4)
即:kx-y+5-4k=0
由
| |2k-1-4k+5| | ||
|
| 3 |
| 4 |
∴切线方程l:3x-4y+8=0
②当切线斜率不存在时,过点P(4,5)的直线为x=4
经检验是圆(x-2)2+(y-1)2=4的切线.
∴切线方程为3x-4y+8=0或x=4.
点评:本题主要考查圆的切线方程,其中根据直线斜率是否存在为分类标准,分别求出圆的切线方程,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
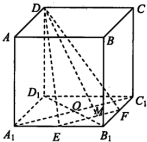 如图,在正方形ABCD=A1B1C1D1中,AB=2,O为底面正方形A1B1C1D1的中心,E、F分别为A1B1、B1C1的中点,点M为EF上一点,且满足
如图,在正方形ABCD=A1B1C1D1中,AB=2,O为底面正方形A1B1C1D1的中心,E、F分别为A1B1、B1C1的中点,点M为EF上一点,且满足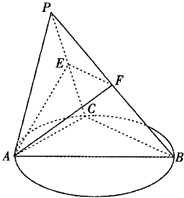 如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F 分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F 分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.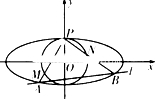 如图,椭圆C:
如图,椭圆C: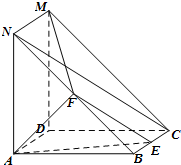 如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.
如图,四边形ABCD与四边形ADMN都为正方形,AN⊥AB,F为线段BN的中点,E为线段BC上的动点.