题目内容
设f(x)满足f(-sinx)+3f(sinx)=4sinx•cosx(|x|≤
).
(1)求f(x)的表达式;
(2)求当x取何值时,f(x)取最大值,并求出最大值.
| π |
| 2 |
(1)求f(x)的表达式;
(2)求当x取何值时,f(x)取最大值,并求出最大值.
考点:函数解析式的求解及常用方法
专题:方程思想,函数的性质及应用
分析:(1)由已知,用sinx代替-sinx,得到关于f(sinx)方程组,求出f(sinx),即得f(x);
(2)求出0≤x≤1时f(x)的最大值以及对应的x的值即可.
(2)求出0≤x≤1时f(x)的最大值以及对应的x的值即可.
解答:
解:(1)∵f(-sinx)+3f(sinx)=4sinx•cosx…①,
∴f(sinx)+3f(-sinx)=-4sinx•cosx…②;
①×3-②得,
8f(sinx)=16sinx•cosx,
又∵|x|≤
,
∴cosx=
,
∴f(x)=2x
(-1≤x≤1);
(2)∵对0≤x≤1,把函数f(x)=2x
化为
f(x)=2
=2
=2
,
令x2=
,则x=
,或x=-
(舍),
∴当x=
时,f(x)有最大值是f(x)max=f(
)=1.
∴f(sinx)+3f(-sinx)=-4sinx•cosx…②;
①×3-②得,
8f(sinx)=16sinx•cosx,
又∵|x|≤
| π |
| 2 |
∴cosx=
| 1-sin2x |
∴f(x)=2x
| 1-x2 |
(2)∵对0≤x≤1,把函数f(x)=2x
| 1-x2 |
f(x)=2
| x2(1-x2) |
| -x4+x2 |
-(x2-
|
令x2=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴当x=
| ||
| 2 |
| ||
| 2 |
点评:本题考查了函数的性质与应用问题,也考查了求函数最值的问题,解题时应用方程思想,求出方程组的解,是中档题.

练习册系列答案
相关题目
如果
<σ<
,那么下列不等式成立的是( )
| π |
| 4 |
| π |
| 2 |
| A、cosσ<sinσ<tanσ |
| B、tanσ<sinσ<cosσ |
| C、sinσ<cosσ<tanσ |
| D、cosσ<tanσ<sinσ |
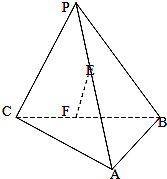 如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )
如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )| A、120° | B、45° |
| C、0° | D、60° |
如果函数y=3cos(2x+φ)的图象关于点(
,0)中心对称,那么ϕ的最小正值为( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=
的最大值是( )
| 1 |
| 3+2sinx+cosx |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
sin110°cos25°-sin20°sin25°=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|