题目内容
已知集合M={x|2014≤x≤2015},N={x|x<a,a∈Z},若“x∈M”是“x∈N”的充分而不必要条件.
(1)求整数a的最小值;
(2)在(1)的条件下,写出命题“若x+2014≤a,则
≥a-2015”的否命题,并判断否命题的真假.
(1)求整数a的最小值;
(2)在(1)的条件下,写出命题“若x+2014≤a,则
| 1 |
| x-1 |
考点:必要条件、充分条件与充要条件的判断,四种命题
专题:集合,简易逻辑
分析:(1)由“x∈M”是“x∈N”的充分而不必要条件,可得M?N,故a>2015,结合a∈Z,可得整数a的最小值;
(2)在(1)的条件下,写出命题“若x+2014≤a,则
≥a-2015”的否命题为“若x>2,则
<1”,由反比例型函数的图象和性质,易判断其真假.
(2)在(1)的条件下,写出命题“若x+2014≤a,则
| 1 |
| x-1 |
| 1 |
| x-1 |
解答:
解:(1)∵集合M={x|2014≤x≤2015},N={x|x<a,a∈Z},
若“x∈M”是“x∈N”的充分而不必要条件.
则M?N,
故a>2015,a∈Z,
故整数a的最小值为2016;
(2)在(1)的条件下,写出命题“若x+2014≤a,则
≥a-2015”的否命题为:
“若x+2014>2016,则
<2016-2015”,
即“若x>2,则
<1”为真命题.
若“x∈M”是“x∈N”的充分而不必要条件.
则M?N,
故a>2015,a∈Z,
故整数a的最小值为2016;
(2)在(1)的条件下,写出命题“若x+2014≤a,则
| 1 |
| x-1 |
“若x+2014>2016,则
| 1 |
| x-1 |
即“若x>2,则
| 1 |
| x-1 |
点评:本题考查的知识点是充要条件,集合的包含关系中的参数问题,四种命题,是逻辑与集合的综合应用,难度不大,属于基础题.

练习册系列答案
相关题目
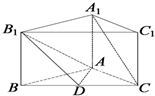 如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中,
如图,正三棱柱(底面是正三角形且侧棱垂直底面的三棱柱)ABC-A1B1C1中,