题目内容
1.若函数y=cos2x与函数y=sin(2x+φ)在[0,$\frac{π}{4}$]上的单调性相同,则φ的一个值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{3π}{2}$ |
分析 由题意可得函数y=sin(2x+φ)在[0,$\frac{π}{4}$]上的单调递减,故2×$\frac{π}{4}$+φ≤2kπ+$\frac{3π}{2}$,且φ≥2kπ+$\frac{π}{2}$,k∈Z,由此求得φ 的范围.
解答 解:由于函数y=cos2x与函数y=sin(2x+φ)在[0,$\frac{π}{4}$]上的单调性相同,
函数y=cos2x在[0,$\frac{π}{4}$]上的单调递减,
故函数y=sin(2x+φ)在[0,$\frac{π}{4}$]上的单调递减,
故 2×$\frac{π}{4}$+φ≤2kπ+$\frac{3π}{2}$,且φ≥2kπ+$\frac{π}{2}$,k∈Z,由此求得$\frac{π}{2}$≤φ≤π,
故选:C.
点评 本题主要考查正弦函数、余弦函数的单调性,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.已知全集U={1,2,3,4,5,6,7},M={1,3,5,7},N={2,5,6,7},则M∪(∁UN)=( )
| A. | {1,3,5,7} | B. | {1,2,4} | C. | {1,3,4,5,7} | D. | {1,3,4,5,6} |
13.若P点是以A(-3,0)、B(3,0)为焦点,实轴长为2$\sqrt{5}$的双曲线与圆x2+y2=9的一个交点,则|PA|+|PB|=( )
| A. | 4$\sqrt{13}$ | B. | 2$\sqrt{14}$ | C. | 2$\sqrt{13}$ | D. | 3$\sqrt{14}$ |
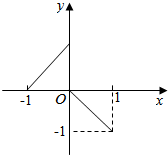 已知函数f(x)的图象如图所示.
已知函数f(x)的图象如图所示.