题目内容
10．
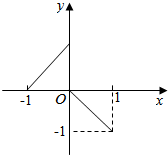已知函数f（x）的图象如图所示．（1）求函数f（x）的解析式；
（2）求函数f（x）的定义域和值域．
分析 （1）使用待定系数法解出；
（2）根据图象最左边到最右边的横坐标范围及定义域，最下边到最上边的纵坐标即为值域，去除取不到的点即可．
解答 解：（1）当-1≤x＜0时，设f（x）=ax+b，则$\left\{\begin{array}{l}{-a+b=0}\\{b=1}\end{array}\right.$，
解得a=1，b=1，∴f（x）=x+1；
当0≤x≤1时，设f（x）=kx，则k=-1，∴f（x）=-x，
∴f（x）的解析式为f（x）=$\left\{\begin{array}{l}{x+1，-1≤x＜0}\\{-x，0≤x≤1}\end{array}\right.$
（2）定义域为[-1，1]，值域为[-1，1）
点评 本题考查了分段函数的解析式与图象，确定x在各段上的取值范围是关键，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
1．若函数y=cos2x与函数y=sin（2x+φ）在[0，$\frac{π}{4}$]上的单调性相同，则φ的一个值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{3π}{4}$ | D． | $\frac{3π}{2}$ |
2．函数f（x）=$\frac{2}{x-1}$，x∈[2，3]的最大值是（ ）
| A． | 2 | B． | 3 | C． | 1 | D． | 5 |