题目内容
若复数z满足3+i=（1+i）z（i为虚数单位），则|z|等于（ ）
| A、5 | ||
| B、3 | ||
C、
| ||
D、
|
考点：复数求模
专题：数系的扩充和复数
分析：利用复数的运算法则和模的计算公式即可得出．
解答：
解：∵复数z满足3+i=（1+i）z（i为虚数单位），
∴z=
=
=
=2-i．
∴|z|=
=
．
故选：C．
∴z=
| 3+i |
| 1+i |
| (3+i)(1-i) |
| (1+i)(1-i) |
| 4-2i |
| 2 |
∴|z|=
| 22+(-1)2 |
| 5 |
故选：C．
点评：本题考查了复数的运算法则和模的计算公式，属于基础题．
练习册系列答案
相关题目
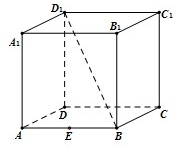正方体AC1中，E为AB的中点，点P为侧面BB1C1C内一动点（含边界），若动点P始终满足PE⊥BD1，则动点P的轨迹是（ ）| A、直线 | B、线段 |
| C、圆的一部分 | D、椭圆的一部分 |
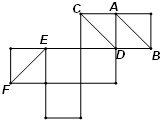如图是一个正方体纸展开图，如果将它还原成正方体，那么直线AB，CD，EF在原正方体的位置关系是（ ）| A、AB∥CD，EF⊥CD |
| B、AB与CD异面成角60°，CD与EF相交成角60° |
| C、AB∥CD，CD与EF相交成角60° |
| D、EF⊥CD，AB与CD异面成角60° |
函数f（x）=x2-ax+2在（2，+∞）上单调递增，则a的取值范围为（ ）
| A、[2，+∞） |
| B、[4，+∞） |
| C、（-∞，4] |
| D、（-∞，-4] |
函数f（x）=x2-x的零点个数是（ ）
| A、3 | B、2 | C、1 | D、0 |
“x=2”是“log2|x|=1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
函数f（x）=lg
的图象（ ）
| 1+sinx |
| cosx |
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |
在平面直角坐标系xOy中，椭圆E：