题目内容
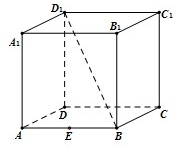正方体AC1中，E为AB的中点，点P为侧面BB1C1C内一动点（含边界），若动点P始终满足PE⊥BD1，则动点P的轨迹是（ ）| A、直线 | B、线段 |
| C、圆的一部分 | D、椭圆的一部分 |
考点：直线与平面垂直的性质
专题：空间位置关系与距离
分析：如图，取BC，BB1的中点F，G．先找到一个平面总是保持与BD1垂直，即BD1⊥面EFG，又点P在侧面BCC1B1及其边界上运动，并且总是保持AP与BD1垂直，得到点P的轨迹为面EFG与面BCC1B1的交线段，结合平面的基本性质知这两个平面的交线是FG．
解答：
解：先找到一个平面总是保持与BD1垂直，
取BC，BB1的中点F，G．连接EF，FG，EG，
在正方体ABCD-A1B1C1D1中，
有BD1⊥面EFG，
又点P在侧面BCC1B1及其边界上运动，
根据平面的基本性质得：
点P的轨迹为面EFG与面BCC1B1的交线段FG．
故选：B．
解：先找到一个平面总是保持与BD1垂直，取BC，BB1的中点F，G．连接EF，FG，EG，
在正方体ABCD-A1B1C1D1中，
有BD1⊥面EFG，
又点P在侧面BCC1B1及其边界上运动，
根据平面的基本性质得：
点P的轨迹为面EFG与面BCC1B1的交线段FG．
故选：B．
点评：本题考查线面垂直的判定与正方体的几何特征、轨迹的求法、平面的基本性质等基础知识，考查空间想象力．属于基础题．
练习册系列答案
相关题目
若抛物线x=-4y2上一点M到焦点F的距离为1，则点M的横坐标为（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
要得到y=sin（
+
）的图象，需将函数y=sin
的图象至少向左平移（ ）个单位．
| x |
| 2 |
| π |
| 3 |
| x |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
以下说法正确的是（ ）
| A、命题“a、b都是有理数”的否定是“a、b都不是有理数” |
| B、设{an}是等比数列，则“a1＜a2”是“数列{an}是递增数列”的充要条件 |
| C、用相关系数r来判断两个变量的相关性时，r越小，说明两个变量的相关性越弱 |
| D、将一组数据中的每个数据加上或减去同一个数后，方差恒不变 |
三段论：“①雅安人一定坚强不屈②雅安人是中国人③所有的中国人都坚强不屈”中，其中“大前提”和“小前提”分别是等于（ ）
| A、①② | B、③① | C、③② | D、②③ |
二项式（x2-
）6的展开式中含x3项的系数是（ ）（用数字作答）
| 2 |
| x |
| A、-160 | B、160 |
| C、-150 | D、150 |
若复数z满足3+i=（1+i）z（i为虚数单位），则|z|等于（ ）
| A、5 | ||
| B、3 | ||
C、
| ||
D、
|