题目内容
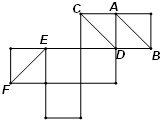如图是一个正方体纸展开图，如果将它还原成正方体，那么直线AB，CD，EF在原正方体的位置关系是（ ）| A、AB∥CD，EF⊥CD |
| B、AB与CD异面成角60°，CD与EF相交成角60° |
| C、AB∥CD，CD与EF相交成角60° |
| D、EF⊥CD，AB与CD异面成角60° |
考点：棱柱的结构特征
专题：空间位置关系与距离
分析：先把正方体的展开图再还原成正方体，进而利用正方体的几何特征，可分析出直线AB，CD，EF的位置关系．
解答：
解：如图所示：把展开图再还原成正方体，
连接DF，EG，DG，
可得△E（C）DG和△DE（C）F均为等边三角形，
故CD与EF相交成60°，
EG与CD相交成60°，
又∵AB∥EG，AB与CD异面，
故AB与CD异面成角60°，
故选：B．
解：如图所示：把展开图再还原成正方体，连接DF，EG，DG，
可得△E（C）DG和△DE（C）F均为等边三角形，
故CD与EF相交成60°，
EG与CD相交成60°，
又∵AB∥EG，AB与CD异面，
故AB与CD异面成角60°，
故选：B．
点评：本题考查正方体的展开图还原成正方体，其中把正方体的展开图再还原成正方体，是解答的关键．
练习册系列答案
相关题目
若抛物线x=-4y2上一点M到焦点F的距离为1，则点M的横坐标为（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
三段论：“①雅安人一定坚强不屈②雅安人是中国人③所有的中国人都坚强不屈”中，其中“大前提”和“小前提”分别是等于（ ）
| A、①② | B、③① | C、③② | D、②③ |
二项式（x2-
）6的展开式中含x3项的系数是（ ）（用数字作答）
| 2 |
| x |
| A、-160 | B、160 |
| C、-150 | D、150 |
已知集合A={0，1，2，3}，B={x|x2-x=0}，则集合A∩B=（ ）
| A、{0} | B、{1，2，3} |
| C、{0，1} | D、{1} |
已知a＞0，x、y满足约束条件
，若z=2x+y的最小值为0，则a=（ ）
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
掷一颗质地均匀的骰子，观察所得的点数a，设事件A=“a为3”，B=“a为4”，C=“a为奇数”，则下列结论正确是（ ）
| A、A与B为互斥事件 |
| B、A与B为对立事件 |
| C、A与C为对立事件 |
| D、A与C为互斥事件 |
若复数z满足3+i=（1+i）z（i为虚数单位），则|z|等于（ ）
| A、5 | ||
| B、3 | ||
C、
| ||
D、
|