题目内容
已知函数f（x）=9-x-2•（
）x．
（1）当x＞0时，求f（x）的值域；
（2）求f（x）的单调减区间．
| 1 |
| 3 |
（1）当x＞0时，求f（x）的值域；
（2）求f（x）的单调减区间．
考点：指数型复合函数的性质及应用,复合函数的单调性
专题：计算题,函数的性质及应用
分析：化简f（x）=9-x-2•（
）x=（3-x-1）2-1，
（1）由x＞0可得0＜3-x＜1，从而确定f（x）的值域；
（2）由复合函数的单调性判断函数的单调性．
| 1 |
| 3 |
（1）由x＞0可得0＜3-x＜1，从而确定f（x）的值域；
（2）由复合函数的单调性判断函数的单调性．
解答：
解：f（x）=9-x-2•（
）x=（3-x-1）2-1，
（1）∵x＞0，∴0＜3-x＜1；
∴-1＜（3-x-1）2-1＜0；
故f（x）的值域为（-1，0）；
（2）由复合函数的单调性可知，
f（x）在（-∞，0）上是减函数，
故f（x）的单调减区间为（-∞，0）．
| 1 |
| 3 |
（1）∵x＞0，∴0＜3-x＜1；
∴-1＜（3-x-1）2-1＜0；
故f（x）的值域为（-1，0）；
（2）由复合函数的单调性可知，
f（x）在（-∞，0）上是减函数，
故f（x）的单调减区间为（-∞，0）．
点评：本题考查了函数的单调性及值域的求法，同时考查了复合函数的单调性的判断，属于基础题．
练习册系列答案
相关题目
已知p：方程
+
=1所表示的曲线为焦点在x轴上的椭圆，q：|t-a|＜2（a∈N），若p是q的充分不必要条件，则a取值范围为（ ）
| x2 |
| 3-t |
| y2 |
| t+1 |
| A、（-∞，1] |
| B、[-1，1] |
| C、[0，+∞） |
| D、（0，1） |
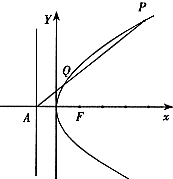抛物线的顶点在原点，焦点在x轴上，准线l与x轴相交于点A（-1，0），过点A的直线与抛物线相交于P、Q两点．