题目内容
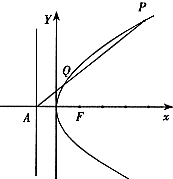 抛物线的顶点在原点,焦点在x轴上,准线l与x轴相交于点A(-1,0),过点A的直线与抛物线相交于P、Q两点.
抛物线的顶点在原点,焦点在x轴上,准线l与x轴相交于点A(-1,0),过点A的直线与抛物线相交于P、Q两点. (1)求抛物线的方程;
(2)若
| FP |
| FQ |
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:计算题,平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)由条件设出抛物线方程,求出准线方程,由交点A,可得p=2,进而得到抛物线方程;
(2)设直线AP:y=k(x+1),代入抛物线方程,消去y,运用韦达定理,再由向量垂直的条件:数量积为0,得到k的方程,解得k,再检验判别式是否大于0,即可得到直线PQ的方程.
(2)设直线AP:y=k(x+1),代入抛物线方程,消去y,运用韦达定理,再由向量垂直的条件:数量积为0,得到k的方程,解得k,再检验判别式是否大于0,即可得到直线PQ的方程.
解答:
解:(1)抛物线的顶点在原点,焦点在x轴上,
可设抛物线方程为y2=2px,准线为x=-
,
由于准线l与x轴相交于点A(-1,0),则
=1,解得p=2,
则抛物线方程为y2=4x;
(2)显然直线AP的斜率不为0,则设直线AP:y=k(x+1),代入抛物线方程,
消去y,得,k2x2+(2k2-4)x+k2=0,
则判别式△=(2k2-4)2-4k4>0,解得,-1<k<1.
x1+x2=
,x1x2=1,y1y2=
=4,
由于
•
=0,则(x1-1)(x2-1)+y1y2=0,
即有x1x2-(x1+x2)+1+4=0,
即6-
=0,解得,k2=
,即k=±
.
检验满足-1<k<1,
则所求直线PQ的方程为:y=±
(x+1).
可设抛物线方程为y2=2px,准线为x=-
| p |
| 2 |
由于准线l与x轴相交于点A(-1,0),则
| p |
| 2 |
则抛物线方程为y2=4x;
(2)显然直线AP的斜率不为0,则设直线AP:y=k(x+1),代入抛物线方程,
消去y,得,k2x2+(2k2-4)x+k2=0,
则判别式△=(2k2-4)2-4k4>0,解得,-1<k<1.
x1+x2=
| 4-2k2 |
| k2 |
| 16x1x2 |
由于
| FP |
| FQ |
即有x1x2-(x1+x2)+1+4=0,
即6-
| 4-2k2 |
| k2 |
| 1 |
| 2 |
| ||
| 2 |
检验满足-1<k<1,
则所求直线PQ的方程为:y=±
| ||
| 2 |
点评:本题考查抛物线的方程和性质,考查直线方程和抛物线方程联立,消去未知数,运用韦达定理,同时考查向量垂直的条件,考查运算能力,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
设集合M={m∈Z|-2<m<3},N={n∈N|-1≤n≤2},则M∩N=( )
| A、{0,1} |
| B、{-1,0,1} |
| C、{0,1,2} |
| D、{-1,0,1,2} |
在平面直角坐标系xOy中,已知
、
是互相垂直的两个单位向量,点Q满足
=3
+4
.曲线C={P|
=2
cosθ+2
sinθ,0≤θ≤2π},区域Ω={P|0<r≤|
|≤R,r<R}.若C∩Ω=C,则( )
| a |
| b |
| OQ |
| a |
| b |
| OP |
| a |
| b |
| PQ |
| A、0<r≤3且R≥7 |
| B、0<r≤3≤R≤7 |
| C、0<r≤5<R<7 |
| D、5≤r<7≤R |
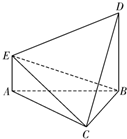 如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2.
如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2.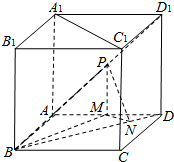 如图,正方体ABCD-A1B1C1D1的棱长为2,点P为面ADD1A1的对角线AD1的中点.PM⊥平面ABCD交AD与M,MN⊥BD于N.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P为面ADD1A1的对角线AD1的中点.PM⊥平面ABCD交AD与M,MN⊥BD于N.