题目内容
已知Sn为等比数列{an}的前n项和,且a1+a4=-
,且对于任意的n∈N*,有Sn、Sn+2、Sn+1成等差数列,{bn}的前n项和Tn=
n2+
n(n∈N*,k>0),且Tn的最小值为1.
(1)求数列{an}和{bn}的通项公式;
(2)对任意m∈N*,将数列{bn}中落入区间(2m+
,4m+
)内的个数记为cm,求数列{cm}的前m项和;
(3)记Pn=|
|+|
|+|
|+…+|
|,若(n-1)2≤m(Pn-n-1)对于n≥2恒成立,求实数m的取值范围.
| 7 |
| 16 |
| 1 |
| 2 |
| k |
| 2 |
(1)求数列{an}和{bn}的通项公式;
(2)对任意m∈N*,将数列{bn}中落入区间(2m+
| 9 |
| 2 |
| 9 |
| 2 |
(3)记Pn=|
| b1 |
| a1 |
| b2 |
| a2 |
| b3 |
| a3 |
| bn |
| an |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由已知得2(a1+a1q+a1q2)=a1+a1+a1q.由此求出an=(-
)n.由已知得T1=b1=
+
=1,解得k=1,当n≥2时,bn=Tn-Tn-1=(
n2+
n)-[
(n-1)2+
(n-1)]=n,从而求出bn=n.
(2)由2m+
<n<4m+
,得数列{bn}中落入区间(2m+
,4m+
)内的个数cm=4m-2m,由此能求出数列{cm}的前m项和.
(3)由|
|=|
|=n•2n,利用错位相减法能求出(n-1)2≤m(Tn-n-1)对于n≥2恒成立的实数m的范围.
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由2m+
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
(3)由|
| bn |
| an |
| n | ||
(-
|
解答:
解:(1)设等比数列{an}的公比为q,
∵对于任意的n∈N*,有Sn、Sn+2、Sn+1成等差数列,
∴2(a1+a1q+a1q2)=a1+a1+a1q.
整理得:2a1(1+q+q2)=a1(2+q).
∵a1≠0,∴2+2q+2q2=2+q.
∴2q2+q=0,又q≠0,∴q=-
.
又a1+a4=a1(1+q3)=-
,
把q=-
代入,得a1=-
.
∴an=a1qn-1=(-
)×(-
)n-1=(-
)n.
∵{bn}的前n项和Tn=
n2+
n(n∈N*,k>0),且Tn的最小值为1.
∴T1=b1=
+
=1,解得k=1,
当n≥2时,bn=Tn-Tn-1=(
n2+
n)-[
(n-1)2+
(n-1)]=n,
n=1时,上式成立,
∴bn=n.
(2)由2m+
<n<4m+
,
得数列{bn}中落入区间(2m+
,4m+
)内的个数cm=4m-2m,
∴数列{cm}的前m项和Sm=(4+42+43+…+4m)-(2+22+23+…+2m)
=
-
=
-2m+1+
.
(3)∵bn=n,an=(-
)n,
∴|
|=|
|=n•2n,
∴Pn=1×2+2×22+3×23+…+n•2n.
2Pn=1×22+2×23+3×24+…+(n-1)•2n+n•2n+1.
∴-Pn=2+22+23+…+2n-n•2n+1=
-n•2n+1,
∴Pn=-(
-n•2n+1)=(n-1)•2n+1+2.
若(n-1)2≤m(Tn-n-1)对于n≥2恒成立,
则(n-1)2≤m[(n-1)•2n+1+2-n-1]对于n≥2恒成立,
也就是(n-1)2≤m(n-1)•(2n+1-1)对于n≥2恒成立,
∴m≥
对于n≥2恒成立,
令f(n)=
,
∵f(n+1)-f(n)=
-
=
<0
∴f(n)为减函数,∴f(n)≤f(2)=
=
.
∴m≥
.
∴(n-1)2≤m(Tn-n-1)对于n≥2恒成立的实数m的范围是[
,+∞).
∵对于任意的n∈N*,有Sn、Sn+2、Sn+1成等差数列,
∴2(a1+a1q+a1q2)=a1+a1+a1q.
整理得:2a1(1+q+q2)=a1(2+q).
∵a1≠0,∴2+2q+2q2=2+q.
∴2q2+q=0,又q≠0,∴q=-
| 1 |
| 2 |
又a1+a4=a1(1+q3)=-
| 7 |
| 16 |
把q=-
| 1 |
| 2 |
| 1 |
| 2 |
∴an=a1qn-1=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵{bn}的前n项和Tn=
| 1 |
| 2 |
| k |
| 2 |
∴T1=b1=
| 1 |
| 2 |
| k |
| 2 |
当n≥2时,bn=Tn-Tn-1=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
n=1时,上式成立,
∴bn=n.
(2)由2m+
| 9 |
| 2 |
| 9 |
| 2 |
得数列{bn}中落入区间(2m+
| 9 |
| 2 |
| 9 |
| 2 |
∴数列{cm}的前m项和Sm=(4+42+43+…+4m)-(2+22+23+…+2m)
=
| 4(1-4m) |
| 1-4 |
| 2(1-2m) |
| 1-2 |
=
| 4m+1 |
| 3 |
| 2 |
| 3 |
(3)∵bn=n,an=(-
| 1 |
| 2 |
∴|
| bn |
| an |
| n | ||
(-
|
∴Pn=1×2+2×22+3×23+…+n•2n.
2Pn=1×22+2×23+3×24+…+(n-1)•2n+n•2n+1.
∴-Pn=2+22+23+…+2n-n•2n+1=
| 2(1-2n) |
| 1-2 |
∴Pn=-(
| 2-2n+1 |
| 1-2 |
若(n-1)2≤m(Tn-n-1)对于n≥2恒成立,
则(n-1)2≤m[(n-1)•2n+1+2-n-1]对于n≥2恒成立,
也就是(n-1)2≤m(n-1)•(2n+1-1)对于n≥2恒成立,
∴m≥
| n-1 |
| 2n+1-1 |
令f(n)=
| n-1 |
| 2n+1-1 |
∵f(n+1)-f(n)=
| n |
| 2n+2-1 |
| n-1 |
| 2n+1-1 |
| (2-n)•2n+1-1 |
| (2n+2-1)(2n+1-1) |
∴f(n)为减函数,∴f(n)≤f(2)=
| 2-1 |
| 23-1 |
| 1 |
| 7 |
∴m≥
| 1 |
| 7 |
∴(n-1)2≤m(Tn-n-1)对于n≥2恒成立的实数m的范围是[
| 1 |
| 7 |
点评:本题考查数列的通项公式、前n项和的求法,考查实数的取值范围的求法,熟练掌握等差数列的通项公式、等比数列的前n项和公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系xOy中,已知
、
是互相垂直的两个单位向量,点Q满足
=3
+4
.曲线C={P|
=2
cosθ+2
sinθ,0≤θ≤2π},区域Ω={P|0<r≤|
|≤R,r<R}.若C∩Ω=C,则( )
| a |
| b |
| OQ |
| a |
| b |
| OP |
| a |
| b |
| PQ |
| A、0<r≤3且R≥7 |
| B、0<r≤3≤R≤7 |
| C、0<r≤5<R<7 |
| D、5≤r<7≤R |
 如图,在几何体ABCDE中,平面ABC⊥平面BCD,AE∥BD,△ABC为边长等于2的正三角形,CD=2
如图,在几何体ABCDE中,平面ABC⊥平面BCD,AE∥BD,△ABC为边长等于2的正三角形,CD=2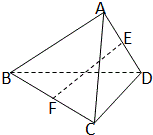 如图,在四面体ABCD中,E、F分别是AD、BC中,AB=CD=2,EF=
如图,在四面体ABCD中,E、F分别是AD、BC中,AB=CD=2,EF=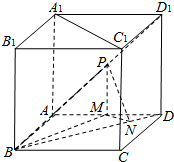 如图,正方体ABCD-A1B1C1D1的棱长为2,点P为面ADD1A1的对角线AD1的中点.PM⊥平面ABCD交AD与M,MN⊥BD于N.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P为面ADD1A1的对角线AD1的中点.PM⊥平面ABCD交AD与M,MN⊥BD于N.