题目内容
已知平面直角坐标系xoy中,动抛物线c:y=2(x-
-3cosθ)2+1+3sinθ(θ任意实数),以Ox轴为极轴建立极坐标系,直线l的极坐标方程是ρcos(θ+
)=0.
(1)写出直线l的直角坐标方程和动抛物线c的顶点的轨迹E的参数方程;
(2)求直线l被曲线E截得的弦长.
| 3 |
| π |
| 6 |
(1)写出直线l的直角坐标方程和动抛物线c的顶点的轨迹E的参数方程;
(2)求直线l被曲线E截得的弦长.
考点:直线与圆锥曲线的综合问题
专题:坐标系和参数方程
分析:(Ⅰ)利用极坐标方程和直角坐标方程的转化公式能求出直线l的直角坐标方程和轨迹E的参数方程.
(Ⅱ)轨迹E的普通方程为(x-
)2+(y-1)2=9,轨迹E为圆,求出圆心D(
,1)到直线l:
x-y=0的距离,由此能求出直线l被曲线E截得的弦长.
(Ⅱ)轨迹E的普通方程为(x-
| 3 |
| 3 |
| 3 |
解答:
解:(Ⅰ)∵直线l的极坐标方程是ρcos(θ+
)=0,
∴直线l的直角坐标方程是
x-y=0,3分
∵动抛物线c:y=2(x-
-3cosθ)2+1+3sinθ(θ任意实数),
∴轨迹E的参数方程是
.(θ为参数).5分
(Ⅱ)轨迹E的普通方程为(x-
)2+(y-1)2=9,轨迹E为圆,6分
则圆心D(
,1)到直线l:
x-y=0的距离d=
=1,7分
所以直线l被曲线E截得的弦长=2
=4
.10分
| π |
| 6 |
∴直线l的直角坐标方程是
| 3 |
∵动抛物线c:y=2(x-
| 3 |
∴轨迹E的参数方程是
|
(Ⅱ)轨迹E的普通方程为(x-
| 3 |
则圆心D(
| 3 |
| 3 |
|
| ||||
| 2 |
所以直线l被曲线E截得的弦长=2
| 9-1 |
| 2 |
点评:本题本题考查对参数方程的理解、表达和与普通方程的互化,也考查了极坐标方程与直角坐标方程的互化.同时考查了直线被圆所截的弦长的求法.

练习册系列答案
相关题目
已知全集U={0,1,2,3,4,5,6},集合A={2,4,5},B={1,3,4,6},则(∁uA)∩B为( )
| A、{0,1,3,6} |
| B、{0,2,4,6} |
| C、{0,1,6} |
| D、{1,3,6} |
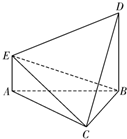 如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2.
如图,在多面体ABCDE中,DB丄平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,BD=2. 如图,在几何体ABCDE中,平面ABC⊥平面BCD,AE∥BD,△ABC为边长等于2的正三角形,CD=2
如图,在几何体ABCDE中,平面ABC⊥平面BCD,AE∥BD,△ABC为边长等于2的正三角形,CD=2