题目内容
14．
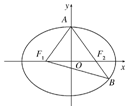如图，已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），F1，F2分别为椭圆的左、右焦点，A为椭圆的上顶点，直线AF2交椭圆于另一点B．（1）若∠F1AB=90°，求椭圆的离心率；
（2）若椭圆的焦距为2，且$\overrightarrow{A{F}_{2}}$=2$\overrightarrow{{F}_{2}B}$，求椭圆的方程．
分析 （1）由△AOF2为等腰直角三角形，则b=c，利用椭圆的离心率公式求得椭圆的离心率；
（2）由$\overrightarrow{A{F}_{2}}$=2$\overrightarrow{{F}_{2}B}$，根据向量数量积的坐标运算，求得B点坐标，代入椭圆方程，即可求得a和b的值，求得椭圆方程．
解答 解：（1）若∠F1AB=90°，则△AOF2为等腰直角三角形．则|OA|=|OF2|，即b=c．
∴a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{2}$c，
椭圆的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$；
（2）由题知2c=2，c=1，则A（0，b），F2（1，0），设B（x，y），
由$\overrightarrow{A{F}_{2}}$=2$\overrightarrow{{F}_{2}B}$，即（1，-b）=2（x-1，y），
∴$\left\{\begin{array}{l}{2x-2=1}\\{2y=-b}\end{array}\right.$，解得x=$\frac{3}{2}$，y=-$\frac{b}{2}$．
代入椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1，即$\frac{9}{4{a}^{2}}+\frac{1}{4}=1$解得a2=3．b2=a2-c2=2，
∴椭圆方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$．
点评 本题考查椭圆的标准方程及简单性质，考查向量的坐标运算，考查计算能力，属于中档题．
练习册系列答案
相关题目
19．已知f（x）是定义在实数集R上的不恒为零的偶函数，且xf（x+1）=（x+1）f（x）对任意实数x恒成立，则$f[f（\frac{5}{2}）]$的值是（ ）
| A． | 0 | B． | $\frac{1}{2}$ | C． | 1 | D． | $\frac{5}{2}$ |
3．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F，椭圆C上的两点A，B关于原点对称，且满足$\overrightarrow{FA}$•$\overrightarrow{FB}$=0，若|FA|=|FB|，则椭圆C的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{3}-1$ | D． | $\frac{\sqrt{3}}{2}$ |