题目内容
2.已知函数f(x)=$\frac{ax}{{x}^{2}+1}$+a,g(x)=aln x-x(a≠0).(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)证明:当a>0时,对于任意x1,x2∈(0,e],总有g(x1)<f (x2)成立,其中e=2.71828…是自然对数的底数.
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)求出f(x)的范围,通过讨论a的范围得到g(x)的单调区间,求出g(x)的最大值,证明结论即可.
解答 解:(Ⅰ)函数f (x)的定义域为R,f′(x)=$\frac{a(1-x2)}{(x2+1)2}$=$\frac{a(1-x)(1+x)}{(x2+1)2}$,
当a>0时,当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + | 0 | - |
| f (x) | ↘ | ↗ | ↘ |
| x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f (x) | ↗ | ↘ | ↗ |
当a>0时,f (x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);
当a<0时,f (x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).
(Ⅱ)由(Ⅰ)可知,当a>0时,f (x)在区间(0,1)上单调递增,f (x)>f (0)=a;
f (x)在区间(1,e]上单调递减,且f (e)=$\frac{ae}{{e}^{2}+1}$+a>a,所以当x∈(0,e]时,f (x)>a,
因为g(x)=aln x-x,所以g′(x)=$\frac{a}{x}$-1,令g′(x)=0,得x=a.
①当a≥e时,g′(x)≥0在区间(0,e]上恒成立,
所以函数g(x)在区间(0,e]上单调递增,所以g(x)max=g(e)=a-e<a.
所以对于任意x1,x2∈(0,e],仍有g(x1)<f(x2).
②当0<a<e时,由g′(x)>0,得0<x<a;由g′(x)<0,得e≥x>a,
所以函数g(x)在区间(0,a)上单调递增,在区间(a,e]上单调递减.
所以g(x)max=g(a)=aln a-a;
因为a-(aln a-a)=a(2-ln a)>a(2-ln e)=a>0,
所以对任意x1,x2∈(0,e],总有g(x1)<f (x2).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.

练习册系列答案
相关题目
10.为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素x,y的含量(单位:毫克),如表是乙厂的5件产品的测量数据:
(1)已知甲厂生产的产品共有98件,求乙厂生产的产品数量;
(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数ξ的分布列及方差.
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数ξ的分布列及方差.
11.记数列{an}的前n项和为Sn,若Sn=3an+1,则a10=( )
| A. | -$\frac{{3}^{9}}{{2}^{10}}$ | B. | -$\frac{{3}^{10}}{{2}^{10}}$ | C. | $\frac{{3}^{9}}{{2}^{10}}$ | D. | $\frac{{3}^{10}}{{2}^{10}}$ |
12.过点M(2,-2p)作抛物线x2=2py(p>0)的两条切线,切点分别为A,B,若线段AB中点的纵坐标为6,则抛物线的方程为( )
| A. | x2=2y | B. | x2=4y | C. | x2=2y或x2=4y | D. | x2=3y或x2=2y |
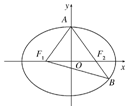 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.