题目内容
6.已知函数{an}满足an+1+1=$\frac{{a}_{n}+1}{2{a}_{n}+3}$,且a1=1,则数列{$\frac{2}{{a}_{n}+1}$}的前20项和为780.分析 利用数列的递推关系式转化求出数列{$\frac{1}{{a}_{n}+1}$}是以$\frac{1}{2}$为首项,2为公差的等差数列,然后求解所求数列的和即可.
解答 解:由an+1+1=$\frac{{a}_{n}+1}{2{a}_{n}+3}$,得$\frac{2{a}_{n}+3}{{a}_{n}+1}=\frac{1}{{a}_{n+1}+1}$,即$\frac{1}{{a}_{n+1}+1}-\frac{1}{{a}_{n}+1}=2$,
∴数列{$\frac{1}{{a}_{n}+1}$}是以$\frac{1}{2}$为首项,2为公差的等差数列,则$\frac{1}{{a}_{n}+1}=2n-\frac{3}{2}$,
∴数列$\{\frac{2}{{a}_{n}+1}\}$是以1为首项,4为公差的等差数列,
其前20项的和为:20+10×19×4=780.
故答案为:780.
点评 本题考查数列的递推关系式的应用,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.记数列{an}的前n项和为Sn,若Sn=3an+1,则a10=( )
| A. | -$\frac{{3}^{9}}{{2}^{10}}$ | B. | -$\frac{{3}^{10}}{{2}^{10}}$ | C. | $\frac{{3}^{9}}{{2}^{10}}$ | D. | $\frac{{3}^{10}}{{2}^{10}}$ |
16.设偶函数f(x)满足f(x)=log4(x+2)-1(x≥0),则{x|f(x-2)>0}等于( )
| A. | {x|x<-2或x>4} | B. | {x|x<0或x>4} | C. | {x|x<0或x>6} | D. | {x|x<-2或x>2} |
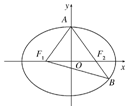 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.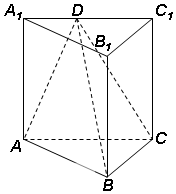 已知在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC⊥BC,BC=C1C=$\frac{1}{2}AC$=1,D是A1C1上的一点,且C1D=kA1C1.
已知在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC⊥BC,BC=C1C=$\frac{1}{2}AC$=1,D是A1C1上的一点,且C1D=kA1C1.