题目内容
9．求不定积分∫$\frac{dx}{{x}^{2}\sqrt{{x}^{2}-4}}$．分析 换元x=$\frac{1}{t}$，则dx=（-$\frac{1}{{t}^{2}}$）dt，则原式═-∫$\frac{t}{\sqrt{1-4{t}^{2}}}$dt=$\frac{1}{8}$∫$\frac{1}{\sqrt{1-4{t}^{2}}}$d（1-4t2）=$\frac{1}{4}$$\sqrt{1-4{t}^{2}}$+C，再将t转化成x．
解答 解：令x=$\frac{1}{t}$，则dx=（-$\frac{1}{{t}^{2}}$）dt，
∫$\frac{dx}{{x}^{2}\sqrt{{x}^{2}-4}}$=∫$\frac{1}{\frac{1}{{t}^{2}}\sqrt{\frac{1}{{t}^{2}}-4}}$（-$\frac{1}{{t}^{2}}$）dt=-∫$\frac{t}{\sqrt{1-4{t}^{2}}}$dt，
=$\frac{1}{8}$∫$\frac{1}{\sqrt{1-4{t}^{2}}}$d（1-4t2），
=$\frac{1}{4}$$\sqrt{1-4{t}^{2}}$+C，
=$\frac{\sqrt{{x}^{2}-4}}{4x}$+C，
∫$\frac{dx}{{x}^{2}\sqrt{{x}^{2}-4}}$=$\frac{\sqrt{{x}^{2}-4}}{4x}$+C．
点评 本题考查微积分基本定理，考查不定积分运算，考查换元法，属于中档题．
练习册系列答案
相关题目
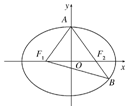如图，已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），F1，F2分别为椭圆的左、右焦点，A为椭圆的上顶点，直线AF2交椭圆于另一点B．
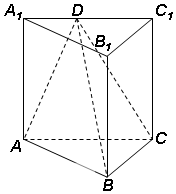已知在三棱柱ABC-A1B1C1中，侧棱垂直于底面，AC⊥BC，BC=C1C=$\frac{1}{2}AC$=1，D是A1C1上的一点，且C1D=kA1C1．