题目内容
3.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足$\overrightarrow{FA}$•$\overrightarrow{FB}$=0,若|FA|=|FB|,则椭圆C的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{3}-1$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由题意可知:△AFB为等腰直角三角形,则A,B位于椭圆的短轴的端点,可得a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{2}$c,根据离心率公式即可求得椭圆C的离心率.
解答  解:由$\overrightarrow{FA}$•$\overrightarrow{FB}$=0,则$\overrightarrow{FA}$⊥$\overrightarrow{FB}$,
解:由$\overrightarrow{FA}$•$\overrightarrow{FB}$=0,则$\overrightarrow{FA}$⊥$\overrightarrow{FB}$,
由|FA|=|FB|,则△AFB为等腰直角三角形,
则A,B位于椭圆的短轴的端点,
则a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{2}$c,
∴椭圆C的离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
故选B.
点评 本题考查椭圆的简单几何性质,考查向量的垂直的充要条件,考查计算能力,属于基础题.

练习册系列答案
相关题目
10.为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中的微量元素x,y的含量(单位:毫克),如表是乙厂的5件产品的测量数据:
(1)已知甲厂生产的产品共有98件,求乙厂生产的产品数量;
(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数ξ的分布列及方差.
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
(2)当产品中的微量元素x,y满足x≥175,且y≥75时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数ξ的分布列及方差.
11.记数列{an}的前n项和为Sn,若Sn=3an+1,则a10=( )
| A. | -$\frac{{3}^{9}}{{2}^{10}}$ | B. | -$\frac{{3}^{10}}{{2}^{10}}$ | C. | $\frac{{3}^{9}}{{2}^{10}}$ | D. | $\frac{{3}^{10}}{{2}^{10}}$ |
8.已知i为虚数单位,复数$z=\frac{1+2i}{i-1}$,则复数z的虚部是( )
| A. | $-\frac{3}{2}i$ | B. | $-\frac{3}{2}$ | C. | $\frac{3}{2}i$ | D. | $\frac{3}{2}$ |
12.过点M(2,-2p)作抛物线x2=2py(p>0)的两条切线,切点分别为A,B,若线段AB中点的纵坐标为6,则抛物线的方程为( )
| A. | x2=2y | B. | x2=4y | C. | x2=2y或x2=4y | D. | x2=3y或x2=2y |
13.若曲线y=x2+ax+b在点(0,b)处的切线方程是3x-y+1=0,则( )
| A. | a=-3,b=1 | B. | a=3,b=1 | C. | a=-3,b=-1 | D. | a=3,b=-1 |
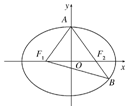 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.