题目内容
4.抛物线y2=-8x中,以(-1,1)为中点的弦所在的直线方程为4x+y+3=0.分析 先设出弦的两端点的坐标然后代入到抛物线方程后两式相减,可求得直线方程的斜率,最后根据直线的点斜式可求得方程.
解答 解:此弦不垂直于x轴,故设点(-1,1)为中点的抛物线y2=-8x的弦的两端点为A(x1,y1)B(x2,y2)
得到yi2=-8x1,y22=-8x2,
两式相减得到(y1+y2)(y1-y2)=-8(x1-x2),
∵y1+y2=2,
∴k=-4,
∴直线方程为y+1=-4(x-1),即4x+y+3=0,
故答案为:4x+y+3=0.
点评 本题主要考查直线和抛物线的综合问题.考查综合运用能力.

练习册系列答案
相关题目
12.过点M(2,-2p)作抛物线x2=2py(p>0)的两条切线,切点分别为A,B,若线段AB中点的纵坐标为6,则抛物线的方程为( )
| A. | x2=2y | B. | x2=4y | C. | x2=2y或x2=4y | D. | x2=3y或x2=2y |
16.设偶函数f(x)满足f(x)=log4(x+2)-1(x≥0),则{x|f(x-2)>0}等于( )
| A. | {x|x<-2或x>4} | B. | {x|x<0或x>4} | C. | {x|x<0或x>6} | D. | {x|x<-2或x>2} |
13.若曲线y=x2+ax+b在点(0,b)处的切线方程是3x-y+1=0,则( )
| A. | a=-3,b=1 | B. | a=3,b=1 | C. | a=-3,b=-1 | D. | a=3,b=-1 |
14.来自英、法、日、德的甲、乙、丙、丁四位客人,刚好碰在一起,他们除懂本国语言外,每天还会说其他三国语言的一种,有一种语言是三人都会说的,但没有一种语言人人都懂,现知道:
①甲是日本人,丁不会说日语,但他俩都能自由交谈;
②四人中没有一个人既能用日语交谈,又能用法语交谈;
③甲、乙、丙、丁交谈时,找不到共同语言沟通;
④乙不会说英语,当甲与丙交谈时,他都能做翻译.针对他们懂的语言
正确的推理是( )
①甲是日本人,丁不会说日语,但他俩都能自由交谈;
②四人中没有一个人既能用日语交谈,又能用法语交谈;
③甲、乙、丙、丁交谈时,找不到共同语言沟通;
④乙不会说英语,当甲与丙交谈时,他都能做翻译.针对他们懂的语言
正确的推理是( )
| A. | 甲日德、乙法德、丙英法、丁英德 | B. | 甲日英、乙日德、丙德法、丁日英 | ||
| C. | 甲日德、乙法德、丙英德、丁英德 | D. | 甲日法、乙英德、丙法德、丁法英 |
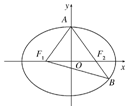 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.