题目内容

已知实数1，m，9成等比数列，则圆锥曲线
x2
m
+y2=1的离心率为（　　）
A、A、B、B、C、C、D、D、
考点：椭圆的简单性质,双曲线的简单性质
专题：等差数列与等比数列,圆锥曲线的定义、性质与方程
分析：首先根据等比中项求出m的值，然后把方程进行分类讨论通过建立方程求得相应的结果．
解答： 解：已知实数1，m，9成等比数列
m2=9 解得m=±3
（1）当m=3时
圆锥曲线
x2
m
+y2=1是椭圆
解得a=
3
 c=
2
则离心率为：
6
3

（2）当m=3时
圆锥曲线
x2
m
+y2=1是双曲线
解得a=1  c=2则离心率为：2
故选：C
点评：本题考查的知识点：等比数列的比例中项，圆锥曲线的方程，椭圆方程及双曲线方程和相关的运算．
练习册系列答案
相关题目
已知，△ABC三个顶点为A（4，1）、B（2，-1）、C（0，5），点D在AB上，
AD
=2
DB
，点E在AC上，要使DE平分△ABC的面积，则点E的坐标为
 
．
已知k∈R，则两条动直线kx-y+2（k+1）=0与x+ky+2（k-1）=0的交点P的轨迹方程为
 
．
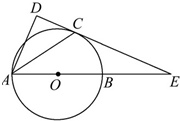如图，已知AB是⊙O的直径，锐角∠DAB的平分线AC交⊙O于点C，作CD⊥AD，垂足为D，直线CD与AB的延长线交于点E．
（1）求证：直线CD为⊙O的切线；
（2）当AB=2BE，且CE=
3
时，求AD的长．
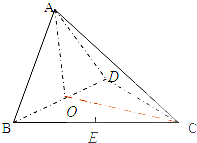如图，在三棱锥A-BCD中，AO⊥平面BCD；O，E分别是BD，BC的中点，CA=CB=CD=BD=2，AB=AD=
2
．
（1）求异面直线AB与CD所成角的余弦值；
（2）求点E到平面ACD的距离．
已知直线C1：2x+4y=5-3m与C2：2x+my=8垂直，垂足为点A．
（1）求实数m的值及点A的坐标；
（2）求过点A且与直线x-y-7=0平行的直线C的方程．
a，b是异面直线，点P∉a∪b，下列命题：
（1）过P可作平面与a，b均平行；
（2）过P可作直线与a，b都相交；
（3）过P可作平面与a，b都垂直；
（4）过P可作直线a，b都垂直，
其中真命题的个数是（　　）
A、1B、2C、3D、4
（1）若函数f（x）=2x2-ax-1在（0，1）内存在x0，使得f（x0）=0，求a的取值范围．
（2）方程mx2+2（m+3）x+2m+14=0有两相异实根，一个大于4，一个小于4，求m的取值范围．
己知长方体的三条棱长分别为a、b、c，其外接球的半径为
3
2

（Ⅰ）求长方体体积的最大值；
（Ⅱ）设
m
=（1，3，
6
），
n
=（a，b，c），求
m
•
n
的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网