题目内容
已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61.
(1) 求a与b的夹角θ;
(2) 求|a+b|;
(3) 若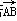 =a,
=a,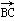 =b,求△ABC的面积.
=b,求△ABC的面积.
解:(1) ∵ (2a-3b)·(2a+b)=61,
∴ 4|a|2-4a·b-3|b|2=61.
又|a|=4,|b|=3,∴ 64-4a·b-27=61,
∴ a·b=-6.
∴ cosθ= =
= =-
=- .
.
又0≤θ≤π,∴ θ= .
.
(2) 可先平方转化为向量的数量积.
|a+b|2=(a+b)2=|a|2+2a·b+|b|2
=42+2×(-6)+32=13,
∴ |a+b|= .
.
(3) ∵ 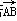 与
与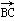 的夹角θ=
的夹角θ= ,
,
∴ ∠ABC=π- =
= .
.
又| |=|a|=4,|
|=|a|=4,|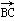 |=|b|=3,
|=|b|=3,
∴ S△ABC= |
|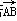 ||
||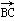 |sin∠ABC=
|sin∠ABC= ×4×3×
×4×3× =3
=3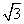 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +i的共轭复数为________.
+i的共轭复数为________. (i是虚数单位),则|z|=________.
(i是虚数单位),则|z|=________.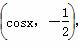 ,b=(
,b=(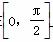 上的最大值和最小值.
上的最大值和最小值. ,
, (xy≠0),则4x+y的最小值是________.
(xy≠0),则4x+y的最小值是________.