题目内容
已知向量a＝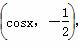
，b＝(
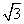sinx，cos2x)，x∈R, 设函数f(x)＝a·b.
(1) 求f (x)的最小正周期.
(2) 求f (x) 在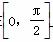
上的最大值和最小值．
解：(1) f(x)＝a·b＝cos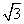x·sinx－
cos2x＝
sin2x－cos2x＝sin
.最小正周期T＝
＝π.
所以f(x)＝sin，最小正周期为π.
(2) 当x∈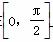时，∈
，由标准函数y＝sinx在上的图象知，
f(x)＝sin∈
＝
.
所以，f (x) 在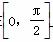上的最大值和最小值分别为1，－.
练习册系列答案
相关题目
＋(m2－5m－6)i(m∈R)，试求实数m分别取什么值时，z分别为：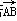
＝a，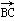
＝b，求△ABC的面积．
的范围是__________．
B. 
D．8π