题目内容
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值.
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
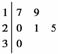
解析: (1)由茎叶图可知,样本数据为17,19,20,21,25,30,则 =
=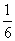 (17+19+20+21+25+30)=22,故样本均值为22.
(17+19+20+21+25+30)=22,故样本均值为22.
(2)日加工零件个数大于样本均值的工人有2名,故优秀工人的频率为 =
= ,该车间12名工人中优秀工人大约有12×
,该车间12名工人中优秀工人大约有12× =4(名),故该车间约有4名优秀工人.
=4(名),故该车间约有4名优秀工人.
(3)记“恰有1名优秀工人”的事件A,其包含的基本事件总数为4×8=32,所有基本事件的总数为 =66,由古典概型概率公式,得P(A)=
=66,由古典概型概率公式,得P(A)= =
= .
.
所以恰有1名优秀工人的概率为 .
.

练习册系列答案
相关题目
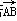 =a,
=a,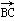 =b,求△ABC的面积.
=b,求△ABC的面积.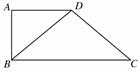
 甲、
甲、
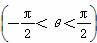 的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P
的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P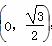 ,则φ的值可以是( )
,则φ的值可以是( )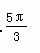 B.
B. 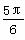
 D.
D. 
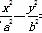 =1和椭圆
=1和椭圆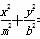 =1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a,b,m为边长的三角形是( )