题目内容
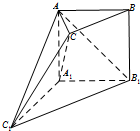 如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.
如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.(Ⅰ)求证:A1C⊥B1C1;
(Ⅱ)若AA1=A1B1=2,且∠B1A1C1=120°,求多面体ABC-A1B1C1的体积.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(Ⅰ)取B1C1的中点D,连接CD、A1D,由已知得四边形CDB1B是平行四边形,CD∥AA1,AA1⊥B1C1,B1C1⊥A1D,由此能证明A1C⊥B1C1.
(Ⅱ)由已知得平面ABC∥平面A1B1D,从而多面体ABC-A1B1D是三棱柱,由此能求出多面体ABC-A1B1C1的体积.
(Ⅱ)由已知得平面ABC∥平面A1B1D,从而多面体ABC-A1B1D是三棱柱,由此能求出多面体ABC-A1B1C1的体积.
解答:
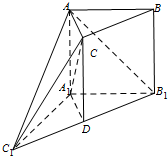 (Ⅰ)证明:取B1C1的中点D,连接CD、A1D,因为BC∥B1C1,B1C1=2BC,
(Ⅰ)证明:取B1C1的中点D,连接CD、A1D,因为BC∥B1C1,B1C1=2BC,
所以CB∥DB1,∴CB=DB1,
∴四边形CDB1B是平行四边形,(1分)
又AA1B1B是矩形,∴CD∥AA1,(2分)
因为侧面AA1B1B⊥底面A1B1C1,AA1⊥A1B1,
∴AA1⊥底面A1B1C1,
∴AA1⊥B1C1,(3分)
因为点D是B1C1的中点,
∴B1C1⊥A1D,(4分)
又A1D∩AA1=A1,∴B1C1⊥平面AA1DC,(5分)
∴A1C⊥B1C1;(6分)
(Ⅱ)解:由(Ⅰ)知:CD∥AA1∥BB1,且CD=AA1=BB1,
∵AB∥A1B1,BC∥B1D1,(7分)
∴平面ABC∥平面A1B1D,(8分)
∴多面体ABC-A1B1D是三棱柱,(9分)
又AA1⊥底面A1B1C1,
∵AA1=AB=2,∠B1A1C1=120°,
∴A1D=1,B1D=
,(10分)
∴三棱柱ABC-A1B1D的体积V1=
A1D•B1D•AA1=
,(11分)
∵B1C1⊥平面AA1CD,
∴四棱锥C1-AA1CD的体积V1=
•A1D•AA1•C1D=
,(12分)
∴多面体ABC-A1B1C1的体积为
.(13分)
 (Ⅰ)证明:取B1C1的中点D,连接CD、A1D,因为BC∥B1C1,B1C1=2BC,
(Ⅰ)证明:取B1C1的中点D,连接CD、A1D,因为BC∥B1C1,B1C1=2BC,所以CB∥DB1,∴CB=DB1,
∴四边形CDB1B是平行四边形,(1分)
又AA1B1B是矩形,∴CD∥AA1,(2分)
因为侧面AA1B1B⊥底面A1B1C1,AA1⊥A1B1,
∴AA1⊥底面A1B1C1,
∴AA1⊥B1C1,(3分)
因为点D是B1C1的中点,
∴B1C1⊥A1D,(4分)
又A1D∩AA1=A1,∴B1C1⊥平面AA1DC,(5分)
∴A1C⊥B1C1;(6分)
(Ⅱ)解:由(Ⅰ)知:CD∥AA1∥BB1,且CD=AA1=BB1,
∵AB∥A1B1,BC∥B1D1,(7分)
∴平面ABC∥平面A1B1D,(8分)
∴多面体ABC-A1B1D是三棱柱,(9分)
又AA1⊥底面A1B1C1,
∵AA1=AB=2,∠B1A1C1=120°,
∴A1D=1,B1D=
| 3 |
∴三棱柱ABC-A1B1D的体积V1=
| 1 |
| 2 |
| 3 |
∵B1C1⊥平面AA1CD,
∴四棱锥C1-AA1CD的体积V1=
| 1 |
| 3 |
2
| ||
| 3 |
∴多面体ABC-A1B1C1的体积为
5
| ||
| 3 |
点评:本题考查异面直线垂直的证明,考查多面体的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
 随着经济的发展,到某岛进行旅游观光的人数越来越多,交通问题已成为制约经济发展的重要因素,因此政府欲在大陆和岛屿之间(如图)建立一条高速通道以便于大陆和岛屿之间来往,大陆沿海线可近似看作函数f(x)=ax(a>1)的图象,且正好与直线y=x相切,而岛屿海岸线可近似看作函数g(x)=loga(x-3)(a>1)的图象.(每单位代表十万米)
随着经济的发展,到某岛进行旅游观光的人数越来越多,交通问题已成为制约经济发展的重要因素,因此政府欲在大陆和岛屿之间(如图)建立一条高速通道以便于大陆和岛屿之间来往,大陆沿海线可近似看作函数f(x)=ax(a>1)的图象,且正好与直线y=x相切,而岛屿海岸线可近似看作函数g(x)=loga(x-3)(a>1)的图象.(每单位代表十万米)
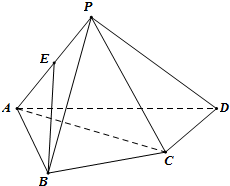 在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)
在四棱锥P-ABCD中,AB⊥BC,AC⊥CD,AB=BC,∠ADc=60°(即:底面是一幅三角板拼成)