有3位同学参加测试.假设每位同学能通过测试的概率都是13.且各人能否通过测试是相互独立的.则至少有一位同学能通过测试的概率为( ) A.827B.49C.23D.1927 题目和参考答案——青夏教育精英家教网—

题目内容

有3位同学参加测试，假设每位同学能通过测试的概率都是

，且各人能否通过测试是相互独立的，则至少有一位同学能通过测试的概率为（　　）

A、

B、

C、

D、

考点：相互独立事件的概率乘法公式,互斥事件的概率加法公式

专题：概率与统计

分析：先求出所有的同学都没有通过的概率，再用1减去此概率，即得所求．

解答： 解：所有的同学都没有通过的概率为(1-

)3=

，
故至少有一位同学能通过测试的概率为 1-

故选：D．

点评：本题主要考查相互独立事件的概率乘法公式，所求的事件与它的对立事件概率间的关系，属于中档题．

练习册系列答案

，2]使不等式f（x）＜mx成立，求实数m的取值范围．

已知等差数列{a_n}的公差是2，前n项和S_n=pn²+2n，n∈N^*．
（Ⅰ）求p的值及数列{a_n}的通项公式；
（Ⅱ）在等比数列{b_n}中，b₂=a₂-2，b₃=a₃+2，数列{b_n}前n项和是T_n，求证：数列{T_n+

}是等比数列．

某班50名学生在一次百米跑测试中，成绩全部介于13秒与18秒之间，将测度结果按如下方式分成五组：第一组[13，14），第二组[14，15），…第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
（Ⅰ）分别求该班成绩在[13，14），[17，18]上的学生人数；
（Ⅱ）如果每次从成绩在[13，14）∪[17，18]上的同学中随机抽取2人，并用m，n分别表示被抽到的两位同学的百米测试成绩，若随机抽取3次（每次抽后都放回），设事件“|m-n|＞1”发生的次数为ξ，求ξ的分布列及数学期望．

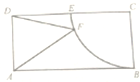如图，矩形ABCD中，AB=2，BC=1，以点C为圆心，CB为半径的圆与边DC交于点E，F是

上任意一点（包括端点），在矩形ABCD内随机取一点M，则点M落在△AFD内部的概率的取值范围是

．

已知a_n=log_n+1（n+2）（n∈N₊），把使得乘积a₁•a₂•a₃…a_n的整数的数n叫做“穿越数”，并把这些“穿越数”由小到大排序构成的数列记为{b_n}（m∈N₊）
（1）求区间（1，2015）内的所有“穿越数”的和；
（2）证明：

+…+

＜

．

某民营企业每年度清理排污费用24万元，为了环保和节省开支，决定安排一个可使用15年的排污设备，安装设备的费用（万元）与设备容量（kw）成正比例，比例系数为0.5，安装设备后企业每年治污的费用w（万元）与该设备容量x（kw）之间的函数关系式是w（x）=

20x+100

（k为常数，x≥0），设F（万元）为该企业安装设备的费用与15年所有治污费用的和．
（1）求k的值，并写出与x的关系式；
（2）当x为何值时，F有最小值？并求出最小值是多少？

过双曲线

=1（a＞0，b）的右焦点F（c，0）的直线交双曲线于A、B两点，交y轴于点P，则有

试题分类