题目内容
14.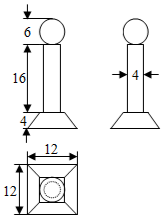 如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.(Ⅰ)求这个酱的体积(π取3.14);
(Ⅱ)求这个奖杯底座的侧面积.
分析 根据三视图知几何体是一个组合体:上面是球、中间是圆柱、下面是正四棱台,并对应的数据,
(Ⅰ)根据球体、柱体和台体的体积公式分别计算,再求和即可;
(Ⅱ)由条件先求出正四棱台的斜高,由梯形的面积公式求出奖杯底座的侧面积.
解答 解:根据三视图知几何体是一个组合体:上面是球、中间是圆柱、下面是正四棱台,
球的半径是3;圆柱的底面半径是2、母线长是16;
正四棱台上底、下底分别为6、12,高为4,
(Ⅰ)球的体积V球=$\frac{4}{3}π{r}^{3}$=$\frac{4}{3}×π×{3}^{3}$=36π(cm3);
圆柱的体积V圆柱=π×22×16=64π(cm3);
V正四棱台=$\frac{1}{3}$×(${6}^{2}+1{2}^{2}+\sqrt{{6}^{2}×1{2}^{2}}$)×4=336(cm3),
所以此奖杯的体积是V=100π+336≈650(cm3);
(Ⅱ)底座是正四棱台,它的斜高是$\sqrt{(6-3)^{2}+{4}^{2}}$=5(cm),
这个奖杯底座的侧面积S=$\frac{1}{2}×(6+12)×5×4$=180(cm2).
点评 本题考查了由三视图求几何体的体积和表面积,考查空间想象能力、运算能力,三视图正确复原几何体是解题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
4.复数$\frac{1-i}{1-2i}$的虚部为( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{3}{5}$ |
9.设函数fn′(x)是fn(x)的导函数,f0(x)=ex(cosx+sinx),f1(x)=$\frac{f_0^'(x)}{{\sqrt{2}}}$,f2(x)=$\frac{f_1^'(x)}{{\sqrt{2}}}$,…,${f_{n+1}}(x)=\frac{f_n^'(x)}{{\sqrt{2}}}$(n∈N),则f2016(x)=( )
| A. | ex(cosx+sinx) | B. | ex(cosx-sinx) | C. | -ex(cosx+sinx) | D. | ex(sinx-cosx) |
6.已知α是第二象限角,且$sin({\frac{π}{2}+α})=-\frac{{\sqrt{5}}}{5}$,则$\frac{{{{cos}^3}α+sinα}}{{cos({α-\frac{π}{4}})}}$=( )
| A. | $-\frac{{11\sqrt{2}}}{15}$ | B. | $-\frac{{9\sqrt{2}}}{5}$ | C. | $\frac{{9\sqrt{2}}}{5}$ | D. | $\frac{{11\sqrt{2}}}{15}$ |
4.下列函数中周期为$\frac{π}{2}$的偶函数是( )
| A. | y=sin4x | B. | y=cos22x-sin22x | C. | y=tan2x | D. | y=cos2x |