题目内容
6.已知α是第二象限角,且$sin({\frac{π}{2}+α})=-\frac{{\sqrt{5}}}{5}$,则$\frac{{{{cos}^3}α+sinα}}{{cos({α-\frac{π}{4}})}}$=( )| A. | $-\frac{{11\sqrt{2}}}{15}$ | B. | $-\frac{{9\sqrt{2}}}{5}$ | C. | $\frac{{9\sqrt{2}}}{5}$ | D. | $\frac{{11\sqrt{2}}}{15}$ |
分析 由诱导公式求出cosα,再由同角三角函数关系式求出tanα,由此利用三角函数加法定理能求出结果.
解答 解:由$sin({\frac{π}{2}+α})=-\frac{{\sqrt{5}}}{5}$,得$cosα=-\frac{{\sqrt{5}}}{5}$,
又∵α是第二象限角,∴tanα=-2,
∴$\frac{{{{cos}^3}α+sinα}}{{cos({α-\frac{π}{4}})}}$=$\frac{{{{cos}^2}α•cosα+sinα}}{{\frac{{\sqrt{2}}}{2}({cosα+sinα})}}=\sqrt{2}•\frac{{{{cos}^2}α+tanα}}{1+tanα}=\frac{{9\sqrt{2}}}{5}$.
故选:C.
点评 本题考查三角函数值的求法,是中档题,解题时要认真审题,注意诱导公式、同角三角函数关系式、三角函数加法定理的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知集合A={2,3,4},B={2,4,6},则A∩B=( )
| A. | {3,6} | B. | {2,4} | C. | {3,4} | D. | {4,6} |
1.完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完成这件事的不同办法数是各类不同方法种数的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分成几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分步计数原理,也叫做乘法原理.
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
小王想获得至少30分的加分,那么概率为多少?
(Ⅱ)某大学的录取分数线为660分,小王估得高考分数可能在630~639,640~649,650~659三个分段.
(1)若小王的高考分数在630~639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个分段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
| 加分 | 人数 |
| 10 | 30 |
| 20 | 90 |
| 30 | 150 |
| 60 | 30 |
(Ⅱ)某大学的录取分数线为660分,小王估得高考分数可能在630~639,640~649,650~659三个分段.
(1)若小王的高考分数在630~639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个分段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
18.将除颜色完全相同的一个白球、一个黄球、两个红球红球分给三个小朋友,且每个小朋友至少分得一个球的分法有 ( )种.
| A. | 15 | B. | 21 | C. | 18 | D. | 24 |
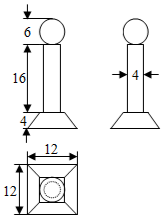 如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.