题目内容
2.在△ABC中,角A,B,C的对边分别为a,b,c,已知a2+c2-b2=ac,且$\sqrt{2}$b=$\sqrt{3}$c.(1)求角A的大小;
(2)设函数f(x)=1+cos(2x+B)-cos2x,求函数f(x)的单调递增区间.
分析 (1)利用余弦定理可得B,再利用正弦定理即可得出;
(2)利用倍角公式、和差公式可得f(x),再利用正弦函数的单调性即可得出.
解答 解:(1)在△ABC中,因为$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{1}{2}$,
所以$B=\frac{π}{3}$.…(2分)
在△ABC中,因为$\sqrt{2}b=\sqrt{3}c$,
由正弦定理可得$\sqrt{2}sinB=\sqrt{3}sinC$,
所以$sinC=\frac{{\sqrt{2}}}{2}$,$0<C<\frac{2π}{3}$,$C=\frac{π}{4}$,
故$A=\frac{2π}{3}-\frac{π}{4}=\frac{5π}{12}$…(6分)
(2)由(1)得$f(x)=1+cos(2x+\frac{π}{3})-cos2x$=$1+\frac{1}{2}cos2x-\frac{{\sqrt{3}}}{2}sin2x-cos2x$=$1-\frac{{\sqrt{3}}}{2}sin2x-\frac{1}{2}cos2x$=$1+sin(2x+\frac{7π}{6})$…(9分)
令$2kπ-\frac{π}{2}≤2x+\frac{7π}{6}≤2kπ+\frac{π}{2}(k∈Z)$,得$kπ-\frac{5π}{6}≤x≤kπ-\frac{π}{3}(k∈Z)$
即函数f(x)的单调递增区间为$[kπ-\frac{5π}{6},kπ-\frac{π}{3}](k∈Z)$…(12分)
点评 本题考查了正弦定理余弦定理、倍角公式、和差公式、正弦函数的单调性即,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.等差数列{an}中,a4+a8=-2,则a6(a2+2a6+a10)的值为( )
| A. | 4 | B. | 8 | C. | -4 | D. | -8 |
13.分别在区间[0,π]和[0,1]内任取两个实数x,y,则不等式y≤sinx恒成立的概率为( )
| A. | $\frac{1}{π}$ | B. | $\frac{2}{π}$ | C. | $\frac{3}{π}$ | D. | $\frac{1}{2}$ |
7.已知全集U=R,集合M={x|0≤x<5},N={x|x≥2},则(∁UN)∩M=( )
| A. | {x|0≤x<2} | B. | {x|0<x≤2} | C. | {x|0<x<2} | D. | {x|0≤x≤2} |
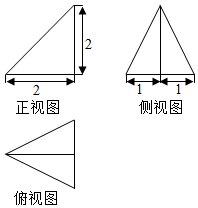
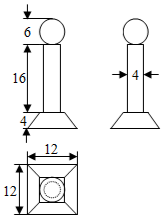 如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.