题目内容
9.设函数fn′(x)是fn(x)的导函数,f0(x)=ex(cosx+sinx),f1(x)=$\frac{f_0^'(x)}{{\sqrt{2}}}$,f2(x)=$\frac{f_1^'(x)}{{\sqrt{2}}}$,…,${f_{n+1}}(x)=\frac{f_n^'(x)}{{\sqrt{2}}}$(n∈N),则f2016(x)=( )| A. | ex(cosx+sinx) | B. | ex(cosx-sinx) | C. | -ex(cosx+sinx) | D. | ex(sinx-cosx) |
分析 我们易得到fn(x)表达式以8为周期,呈周期性变化,由于2016÷8余0,故f2008(x)=f0(x),进而得到答案
解答 解:∵f0(x)=ex(cosx+sinx),
∴f0′(x)=ex(cosx+sinx)+ex(-sinx+cosx)=2excosx,
∴f1(x)=$\frac{f_0^'(x)}{{\sqrt{2}}}$=$\sqrt{2}$excosx,
∴f1′(x)=$\sqrt{2}$ex(cosx-sinx),
∴f2(x)=$\frac{f_1^'(x)}{{\sqrt{2}}}$=ex(cosx-sinx),
∴f2′(x)=ex(cosx-sinx)+ex(-sinx-cosx)=-2exsinx,
∴f3(x)=-$\sqrt{2}$exsinx,
∴f3′(x)=-$\sqrt{2}$ex(sinx+cosx),
∴f4(x)=-ex(cosx+sinx),
∴f4′(x)=-2excosx,
∴f5(x)=-$\sqrt{2}$excosx,
∴f6(x)=-ex(cosx-sinx),
∴f7(x)=$\sqrt{2}$exsinx,
∴f8(x)=ex(cosx+sinx),
…,
∴f2016(x)=f(0)=ex(cosx+sinx),
故选:A.
点评 本题考查的知识点是函数的周期性,函数的值,其中根据已知中的递推式得到fn(x)表达式以8为周期,呈周期性变化,是解答本题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
19.已知集合A={x|y=$\sqrt{x-{x}^{2}}$},B={y|y-1<0},则A∩B=( )
| A. | (-∞,1) | B. | (-∞,1] | C. | [0,1) | D. | [0,1] |
20.已知集合A={x|x2-2x-3>0},B={x|2<x<4},则集合A∩B=( )
| A. | (1,4) | B. | (2,4) | C. | (2,3) | D. | (3,4) |
4.抛物线y2=-4x的焦点坐标是( )
| A. | (-2,0) | B. | (-1,0) | C. | (0,-1) | D. | (0,-2) |
1.完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完成这件事的不同办法数是各类不同方法种数的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分成几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分步计数原理,也叫做乘法原理.
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
小王想获得至少30分的加分,那么概率为多少?
(Ⅱ)某大学的录取分数线为660分,小王估得高考分数可能在630~639,640~649,650~659三个分段.
(1)若小王的高考分数在630~639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个分段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
| 加分 | 人数 |
| 10 | 30 |
| 20 | 90 |
| 30 | 150 |
| 60 | 30 |
(Ⅱ)某大学的录取分数线为660分,小王估得高考分数可能在630~639,640~649,650~659三个分段.
(1)若小王的高考分数在630~639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个分段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
18.将除颜色完全相同的一个白球、一个黄球、两个红球红球分给三个小朋友,且每个小朋友至少分得一个球的分法有 ( )种.
| A. | 15 | B. | 21 | C. | 18 | D. | 24 |
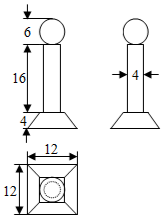 如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.