题目内容
3.多项式(3x+2y)2(x-y)7的展开式中含有x5y4项的系数为-21.分析 多项式(3x+2y)2(x-y)7=(9x2+12xy+4y2)(x-y)7,设(x-y)7的通项公式为Tr+1=${∁}_{7}^{r}$x7-r(-y)r,分别令r=4,r=3,r=2,即可得出.
解答 解:多项式(3x+2y)2(x-y)7=(9x2+12xy+4y2)(x-y)7,
设(x-y)7的通项公式为Tr+1=${∁}_{7}^{r}$x7-r(-y)r,
令r=4,则T5=${∁}_{7}^{4}{x}^{3}(-y)^{4}$=35x3y4,
令r=3,则T4=${∁}_{7}^{3}{x}^{4}(-y)^{3}$=-35x4y3,
令r=2,则T3=${∁}_{7}^{2}$x5(-y)2=21x5y2.
∴多项式(3x+2y)2(x-y)7的展开式中含有x5y4项的系数为:35×9-35×12+21×4=-21.
故答案为:-21.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.分别在区间[0,π]和[0,1]内任取两个实数x,y,则不等式y≤sinx恒成立的概率为( )
| A. | $\frac{1}{π}$ | B. | $\frac{2}{π}$ | C. | $\frac{3}{π}$ | D. | $\frac{1}{2}$ |
18.将除颜色完全相同的一个白球、一个黄球、两个红球红球分给三个小朋友,且每个小朋友至少分得一个球的分法有 ( )种.
| A. | 15 | B. | 21 | C. | 18 | D. | 24 |
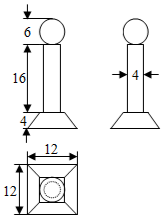 如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.
如图,是一个奖杯的三视图(单位:cm),底座是正四棱台.