题目内容
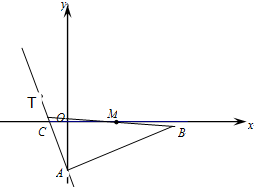 如图,在Rt△ABC中,∠A为直角,AB边所在直线的方程为x-3y-6=0,点T(-1,1)在直线AC上,斜边中点为M(2,0).
如图,在Rt△ABC中,∠A为直角,AB边所在直线的方程为x-3y-6=0,点T(-1,1)在直线AC上,斜边中点为M(2,0).(1)求BC边所在直线的方程;
(2)若动圆P过点N(-2,0),且与Rt△ABC的外接圆相交所得公共弦长为4,求动圆P中半径最小的圆方程.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)先求出AC边所在直线的方程,再求出B,C的坐标,即可求BC边所在直线的方程;
(2)求出Rt△ABC外接圆的方程,设出动圆方程为(x-a)2+(y-b)2=r2,由于⊙P与⊙M相交,则公共弦所在直线的方程m为:(4-2a)x-2by+a2+b2-r2+4=0,利用公共弦长为4,可得r=
=
,即可求动圆P中半径最小的圆方程.
(2)求出Rt△ABC外接圆的方程,设出动圆方程为(x-a)2+(y-b)2=r2,由于⊙P与⊙M相交,则公共弦所在直线的方程m为:(4-2a)x-2by+a2+b2-r2+4=0,利用公共弦长为4,可得r=
| (a+2)2+b2 |
| 4a2+4 |
解答:
解:(1)因为AB边所在直线的方程为x-3y-6=0,AC与AB垂直,所以直线AC的斜率为-3.
故AC边所在直线的方程为y-1=-3(x+1),即3x+y+2=0.
设C为(x0,-3x0-2),
因为M为BC中点,
所以B(4-x0,3x0+2).
点B代入x-3y-6=0,解得x0=-
,所以C(-
,
).
所以BC所在直线方程为:x+7y-2=0.
(2)因为Rt△ABC斜边中点为M(2,0),所以M为Rt△ABC外接圆的圆心.
又AM=2
,从而Rt△ABC外接圆的方程为(x-2)2+y2=8.
设P(a,b),因为动圆P过点N,所以该圆的半径r=
,圆方程为(x-a)2+(y-b)2=r2.
由于⊙P与⊙M相交,则公共弦所在直线的方程m为:(4-2a)x-2by+a2+b2-r2+4=0.
因为公共弦长为4,r=2
,所以M(2,0)到m的距离d=2,即
=2,
化简得b2=3a2-4a,所以r=
=
.
当a=0时,r最小值为2,此时b=0,圆的方程为x2+y2=4.
故AC边所在直线的方程为y-1=-3(x+1),即3x+y+2=0.
设C为(x0,-3x0-2),
因为M为BC中点,
所以B(4-x0,3x0+2).
点B代入x-3y-6=0,解得x0=-
| 4 |
| 5 |
| 4 |
| 5 |
| 2 |
| 5 |
所以BC所在直线方程为:x+7y-2=0.
(2)因为Rt△ABC斜边中点为M(2,0),所以M为Rt△ABC外接圆的圆心.
又AM=2
| 2 |
设P(a,b),因为动圆P过点N,所以该圆的半径r=
| (a+2)2+b2 |
由于⊙P与⊙M相交,则公共弦所在直线的方程m为:(4-2a)x-2by+a2+b2-r2+4=0.
因为公共弦长为4,r=2
| 2 |
| |2(4-2a)+a2+b2-r2+4| | ||
2
|
化简得b2=3a2-4a,所以r=
| (a+2)2+b2 |
| 4a2+4 |
当a=0时,r最小值为2,此时b=0,圆的方程为x2+y2=4.
点评:本题考查直线与直线的位置关系,直线与圆有关知识,考查圆与圆位置关系及弦长的求法及函数最值求法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知动点P(a,b)在不等式组
表示的平面区域内部运动,则
的取值范围是( )
|
| b+3 |
| a-1 |
A、(-
| ||
| B、(-3,2) | ||
C、(-∞,-
| ||
| D、(1,3) |
已知定义域为R的奇函数f(x)的导函数为f′(x),当x≠0时,f′(x)+
>0,若a=
f(
),b=-2f(-2),c=(ln
)f(ln
),则a,b,c的大小关系正确的是( )
| f(x) |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<c<b |
| B、b<c<a |
| C、a<b<c |
| D、c<a<b |
 如图,直三角棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=
如图,直三角棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=