题目内容
在圆内接四边形ABCD中，AC与BD交于点E，过点A作圆的切线交CB的延长线于点F．若AB=AD，AF=18，BC=15，求AE的长．考点：与圆有关的比例线段
专题：选作题,立体几何
分析：由切割线定理，求出FB，再证明四边形ADBF为平行四边形，求出AD=AB，利用
=
，可求AE的长．
| AE |
| AC |
| FB |
| FC |
解答：
解：∵AF是圆的切线，且AF=18，BC=15，
∴由切割线定理可得AF2=FB•FC，
∴182=FB（FB+15），
∴FB=12，
∵AB=AD，
∴∠ABD=∠ADB，
∵AF是圆的切线，
∴∠FAB=∠ADB，
∴∠FAB=∠ABD，
∴AF∥BD，
∵AD∥FC，
∴四边形ADBF为平行四边形，
∴AD=FB=12，
∵∠ACF=∠ADB=∠F，
∴AC=AF=18，
∵
=
，
∴
=
，
∴AE=8．
故答案为：8．
∴由切割线定理可得AF2=FB•FC，
∴182=FB（FB+15），
∴FB=12，
∵AB=AD，
∴∠ABD=∠ADB，
∵AF是圆的切线，
∴∠FAB=∠ADB，
∴∠FAB=∠ABD，
∴AF∥BD，
∵AD∥FC，
∴四边形ADBF为平行四边形，
∴AD=FB=12，
∵∠ACF=∠ADB=∠F，
∴AC=AF=18，
∵
| AE |
| AC |
| FB |
| FC |
∴
| AE |
| 18 |
| 12 |
| 27 |
∴AE=8．
故答案为：8．
点评：本题考查与圆有关的比例线段，考查切割线定理，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
若（9x-
）n（n∈N*）的展开式的第3项的二项式系数为36，则其展开式中的常数项为（ ）
| 1 | ||
3
|
| A、252 | B、-252 |
| C、84 | D、-84 |
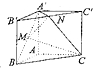如图，直三角棱柱ABC-A′B′C′，∠BAC=90°，AB=AC=