题目内容
已知复数z=
，则|z|=（ ）
| 5 |
| 1+2i |
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、5 |
考点：复数求模
专题：数系的扩充和复数
分析：化简复数，由模长公式可得．
解答：
解：化简可得复数z=
=
=1-2i，
∴|z|=
=
故选：C
| 5 |
| 1+2i |
=
| 5(1-2i) |
| (1+2i)(1-2i) |
∴|z|=
| 12+(-2)2 |
| 5 |
故选：C
点评：本题考查复数的模长，利用复数的基本运算进行化简是解决本题的关键，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
“m=2”是“直线l1：mx+4y-6=0与直线l2：x+my-3=0平行”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若（9x-
）n（n∈N*）的展开式的第3项的二项式系数为36，则其展开式中的常数项为（ ）
| 1 | ||
3
|
| A、252 | B、-252 |
| C、84 | D、-84 |
已知定义域为R的奇函数f（x）的导函数为f′（x），当x≠0时，f′（x）+
＞0，若a=
f（
），b=-2f（-2），c=（ln
）f（ln
），则a，b，c的大小关系正确的是（ ）
| f(x) |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a＜c＜b |
| B、b＜c＜a |
| C、a＜b＜c |
| D、c＜a＜b |
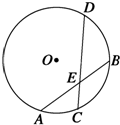如图所示，已知⊙O的半径为5，两弦AB、CD相交于AB的中点E，且AB=8，CE：ED=4：9，则圆心到弦CD的距离为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|