题目内容
一条长为4的线段AB在x轴正半轴上移动，另一条长为2的线段CD在y轴正半轴上移动，如果两条线段的4个端点A、B、C、D四点共圆，那么这个圆的圆心的轨迹是 ．
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：设圆心坐标为（x，y），利用两条线段的4个端点A、B、C、D四点共圆，|AB|=4，|CD|=2，化简可得结论．
解答：
解：设圆心坐标为（x，y），则
∵两条线段的4个端点A、B、C、D四点共圆，|AB|=4，|CD|=2，
∴22+y2=x2+12，
∴x2-y2=3．
故答案为：x2-y2=3．
∵两条线段的4个端点A、B、C、D四点共圆，|AB|=4，|CD|=2，
∴22+y2=x2+12，
∴x2-y2=3．
故答案为：x2-y2=3．
点评：本题考查轨迹方程，考查圆的性质，考查学生的实践能力，属于基础题．
练习册系列答案
相关题目
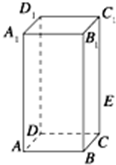如图，正四棱柱ABCD-A1B1C1D1中，AA1=2AB=4，点E在CC1上且C1E=3EC．试建立适当的坐标系，写出点B、C、E、A1的坐标．
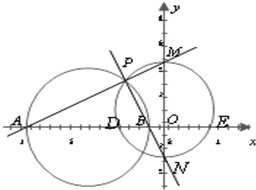如图，已知圆C直径的两个端点坐标分别为A（-9，0）、B（-1，0），点P为圆C上（不同于A、B）的任意一点，连接AP、BP分别交y轴于M、N两点，以MN为直径的圆与x轴交于D、F两点，则弦长|DF|为（ ）