题目内容
一元二次不等式x2-7x+12<0,2x2+x-5>0,x2+2>-2x的解集分别是M、N、P,则M、N、P之间的包含关系是( )
| A、N⊆M⊆P |
| B、M⊆N⊆P |
| C、N⊆P⊆M |
| D、M⊆P⊆N |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:利用一元二次不等式的解法分别得到集合M,N,P.进而判断出三个集合的关系.
解答:
解:一元二次不等式x2-7x+12<0的解集为{x|3<x<4},∴M={x|3<x<4};
2x2+x-5>0的解集为{x|x<
或x>
},∴N={x|x<
或x>
};
x2+2>-2x化为x2+2x+2>0,即(x+1)2+1>0,其解集是R.即P=R.
∵3>
,∴M⊆N.
又N⊆P.
∴M⊆N⊆P.
故选:B.
2x2+x-5>0的解集为{x|x<
-1-
| ||
| 4 |
-1+
| ||
| 4 |
-1-
| ||
| 4 |
-1+
| ||
| 4 |
x2+2>-2x化为x2+2x+2>0,即(x+1)2+1>0,其解集是R.即P=R.
∵3>
-1+
| ||
| 4 |
又N⊆P.
∴M⊆N⊆P.
故选:B.
点评:本题考查了一元二次不等式的解法、集合之间的关系,属于基础题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
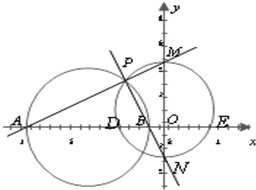 如图,已知圆C直径的两个端点坐标分别为A(-9,0)、B(-1,0),点P为圆C上(不同于A、B)的任意一点,连接AP、BP分别交y轴于M、N两点,以MN为直径的圆与x轴交于D、F两点,则弦长|DF|为( )
如图,已知圆C直径的两个端点坐标分别为A(-9,0)、B(-1,0),点P为圆C上(不同于A、B)的任意一点,连接AP、BP分别交y轴于M、N两点,以MN为直径的圆与x轴交于D、F两点,则弦长|DF|为( )| A、7 | ||
| B、6 | ||
C、2
| ||
D、2
|
下列命题:
(1)若f(x)是增函数,则
是减函数;
(2)若f(x)是减函数,则[f(x)]2是减函数;
(3)若f(x)是增函数,g(x)是减函数,g[f(x)]有意义,则g[f(x)]为减函数,
其中正确的个数有( )
(1)若f(x)是增函数,则
| 1 |
| f(x) |
(2)若f(x)是减函数,则[f(x)]2是减函数;
(3)若f(x)是增函数,g(x)是减函数,g[f(x)]有意义,则g[f(x)]为减函数,
其中正确的个数有( )
| A、1 | B、2 | C、3 | D、0 |
已知一个正三棱锥的三条侧棱两两垂直且相等,底面边长为2,则该三棱锥的外接球的表面积是( )
| A、6π | B、12π |
| C、18π | D、24π |
已知A(-2,0),B(2,0),点P在圆(x-3)2+(y-4)2=4上运动,则|PA|2+|PB|2的最小值是( )
| A、22 | B、10 | C、36 | D、26 |
已知曲线y=2x3上一点A(1,2),则A处切线的斜率是( )
| A、2 | B、3 | C、4 | D、6 |
已知集合A={x|-2≤x≤3},B={x|-1≤x≤4},那么集合A∩B等于( )
| A、{x|-2≤x≤4} |
| B、{x|3≤x≤4} |
| C、{x|-2≤x≤-1} |
| D、{x|-1≤x≤3} |