题目内容
过双曲线C:
-
=1(a>0,b>0)左焦点F且垂直于双曲线一渐近线的直线与双曲线的右支交于点P,O为原点,若|OF|=|OP|,则C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设双曲线的一条渐近线为l:y=-
x,设P(x0,y0),过F作垂直l的直线FP,以及|OF|=|OP|,得到x0,y0的值,再由点P为双曲线的右支上的点,即可算出该双曲线的离心率.
| b |
| a |
解答:
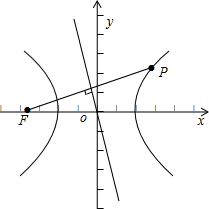 解:设双曲线的一条渐近线为l:y=-
解:设双曲线的一条渐近线为l:y=-
x,设P(x0,y0),
过F(-c,0)作垂直l的直线FP,如图所示,
则FP的直线方程为:y-0=
[x-(-c)],
故y0=
(x0+c) ①,
由于|OF|=|OP|,则FP的中点在直线l:y=-
x上,
则
=-
•
②,
联立①②解得x0=
,y0=
,
又由
-
=1,则
-
=1
整理得到c2-5a2=0,
由此可得双曲线的离心率为e=
=
,
故选:A
 解:设双曲线的一条渐近线为l:y=-
解:设双曲线的一条渐近线为l:y=-| b |
| a |
过F(-c,0)作垂直l的直线FP,如图所示,
则FP的直线方程为:y-0=
| a |
| b |
故y0=
| a |
| b |
由于|OF|=|OP|,则FP的中点在直线l:y=-
| b |
| a |
则
| y0 |
| 2 |
| b |
| a |
| x0-c |
| 2 |
联立①②解得x0=
| b2-a2 |
| c |
| 2ab |
| c |
又由
| x02 |
| a2 |
| y02 |
| b2 |
(
| ||
| a2 |
(
| ||
| b2 |
整理得到c2-5a2=0,
由此可得双曲线的离心率为e=
| c |
| a |
| 5 |
故选:A
点评:本题着重考查了双曲线的标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
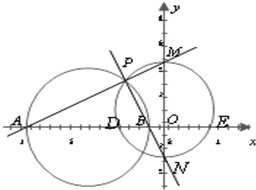 如图,已知圆C直径的两个端点坐标分别为A(-9,0)、B(-1,0),点P为圆C上(不同于A、B)的任意一点,连接AP、BP分别交y轴于M、N两点,以MN为直径的圆与x轴交于D、F两点,则弦长|DF|为( )
如图,已知圆C直径的两个端点坐标分别为A(-9,0)、B(-1,0),点P为圆C上(不同于A、B)的任意一点,连接AP、BP分别交y轴于M、N两点,以MN为直径的圆与x轴交于D、F两点,则弦长|DF|为( )| A、7 | ||
| B、6 | ||
C、2
| ||
D、2
|
在数列{an}中,a1=1,a2=2,若an+2=2an+1-an+2,则an等于( )
A、
| ||||||
| B、n3-5n2+9n-4 | ||||||
| C、n2-2n+2 | ||||||
| D、2n2-5n+4 |
已知实数x、y满足
,则|x+2y-6|-3y的最大值是( )
|
| A、0 | B、2 | C、4 | D、-4.8 |
已知A(-2,0),B(2,0),点P在圆(x-3)2+(y-4)2=4上运动,则|PA|2+|PB|2的最小值是( )
| A、22 | B、10 | C、36 | D、26 |