题目内容
一个几何体的三视图如图所示，则这个几何体的体积为（ ）
A、6
| ||
| B、9 | ||
C、18
| ||
| D、27 |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图知几何体为三棱锥，且三棱锥的高为3，底面三角形底边长为6，该边上的高为3，把数据代入棱锥的体积公式计算．
解答：
解：由三视图知几何体为三棱锥，且三棱锥的高为3，底面三角形底边长为6，该边上的高为3，
∴几何体的体积V=
×
×6×3×3=9．
故选B．
∴几何体的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
故选B．
点评：本题考查了由三视图求几何体的体积，解题的关键是判断几何体的形状及数据所对应的几何量．
练习册系列答案
相关题目
已知p、q是两个命题，若“（￢p）∨q”是假命题，则（ ）
| A、p、q都是假命题 |
| B、p、q都是真命题 |
| C、p是假命题q是真命题 |
| D、p是真命题q是假命题 |
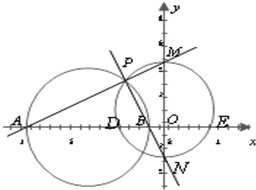如图，已知圆C直径的两个端点坐标分别为A（-9，0）、B（-1，0），点P为圆C上（不同于A、B）的任意一点，连接AP、BP分别交y轴于M、N两点，以MN为直径的圆与x轴交于D、F两点，则弦长|DF|为（ ）| A、7 | ||
| B、6 | ||
C、2
| ||
D、2
|
三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，AC=BC=1，PA=
，则该三棱锥外接球的表面积为（ ）
| 3 |
| A、5π | ||
B、
| ||
| C、20π | ||
| D、4π |
一个直径为32厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高9厘米，则此球的半径为（ ）厘米．
| A、9 | B、10 | C、11 | D、12 |
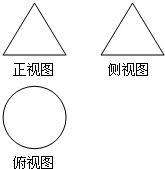如图所示，一个空间几何体的正视图和侧视图都是边长为2的等边三角形，俯视图是一个圆，那么这个几何体的体积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|