题目内容
已知函数y=ax-1-1(a>0切a≠1)的图象恒过点P,角α的终边过点P,则sinα=( )
A、-
| ||||
| B、1 | ||||
C、
| ||||
| D、0 |
考点:任意角的三角函数的定义
专题:三角函数的求值
分析:先求得函数y=ax-1-1(a>0切a≠1)的图象恒过点P(1,0),可得角α的终边过点P(0,1),从而得到x=1,y=0,r=1,再根据 sinα=
求得结果.
| y |
| r |
解答:
解:令x-1=0,求得 x=1 且y=0,
可得函数y=ax-1-1(a>0切a≠1)的图象恒过点P(1,0),
故角α的终边过点P(0,1),
∴x=1,y=0,r=1,
∴sinα=
=0,
故选:D.
可得函数y=ax-1-1(a>0切a≠1)的图象恒过点P(1,0),
故角α的终边过点P(0,1),
∴x=1,y=0,r=1,
∴sinα=
| y |
| r |
故选:D.
点评:本题主要考查指数函数的图象经过定点问题,任意角的三角函数的定义,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
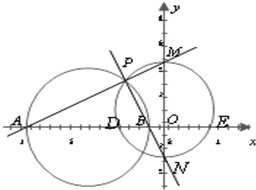 如图,已知圆C直径的两个端点坐标分别为A(-9,0)、B(-1,0),点P为圆C上(不同于A、B)的任意一点,连接AP、BP分别交y轴于M、N两点,以MN为直径的圆与x轴交于D、F两点,则弦长|DF|为( )
如图,已知圆C直径的两个端点坐标分别为A(-9,0)、B(-1,0),点P为圆C上(不同于A、B)的任意一点,连接AP、BP分别交y轴于M、N两点,以MN为直径的圆与x轴交于D、F两点,则弦长|DF|为( )| A、7 | ||
| B、6 | ||
C、2
| ||
D、2
|
在数列{an}中,a1=1,a2=2,若an+2=2an+1-an+2,则an等于( )
A、
| ||||||
| B、n3-5n2+9n-4 | ||||||
| C、n2-2n+2 | ||||||
| D、2n2-5n+4 |
一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米,则此球的半径为( )厘米.
| A、9 | B、10 | C、11 | D、12 |
已知实数x、y满足
,则|x+2y-6|-3y的最大值是( )
|
| A、0 | B、2 | C、4 | D、-4.8 |
下列命题:
(1)若f(x)是增函数,则
是减函数;
(2)若f(x)是减函数,则[f(x)]2是减函数;
(3)若f(x)是增函数,g(x)是减函数,g[f(x)]有意义,则g[f(x)]为减函数,
其中正确的个数有( )
(1)若f(x)是增函数,则
| 1 |
| f(x) |
(2)若f(x)是减函数,则[f(x)]2是减函数;
(3)若f(x)是增函数,g(x)是减函数,g[f(x)]有意义,则g[f(x)]为减函数,
其中正确的个数有( )
| A、1 | B、2 | C、3 | D、0 |
已知曲线y=2x3上一点A(1,2),则A处切线的斜率是( )
| A、2 | B、3 | C、4 | D、6 |
