题目内容
一个圆台的上、下底面积是πcm2和49πcm2，一个平行与底面的截面积为25πcm2，则这个截面与上、下底面的距离之比为（ ）
| A、2：1 | ||
| B、3：1 | ||
C、
| ||
D、
|
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：根据圆台数学底面面积比，求出上下底面半径的比，推出截面与上下底面半径的比，求出圆台扩展为圆锥的高的比，然后求出截面分圆台上下部分的距离之比．
解答：
解：圆台上下两底面的半径比为1：7，截面与底面半径比为5：7，圆台扩展为圆锥，轴截面如图：
所以h2+h3=6h1，h2=4h1；
所以h3=2h1
这个截面与上、下底面的距离之比为：2：1
故选A
所以h2+h3=6h1，h2=4h1；
所以h3=2h1
这个截面与上、下底面的距离之比为：2：1
故选A
点评：本题是基础题，考查圆台有关面积的计算问题，注意面积之比与相似比的平方的关系，轴面积的应用，常考题型．
练习册系列答案
相关题目
已知两个不相等的实数a、b满足以下关系式：a2sinθ+acosθ-
=0，b2sinθ+bcosθ-
=0，则连接A（a2，a）、B（b2，b）两点的直线与圆x2+y2=1的位置关是（ ）
| π |
| 4 |
| π |
| 4 |
| A、相离 | B、相切 |
| C、相交 | D、不能确定 |
已知sinα-cosα=
，则tanα+
=（ ）
| 1 |
| 3 |
| 1 |
| tanα |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=-
x2-3x-
的值域是（ ）
| 1 |
| 2 |
| 5 |
| 2 |
A、{y|y≥-
| ||
B、{y|y≤-
| ||
| C、{y|y≥2} | ||
| D、{y|y≤2} |
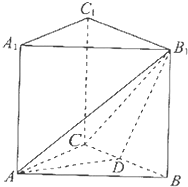如图，在棱长均相等的正三棱柱ABC-A1B1C1中，D为BC的中点．
如图，椭圆C：