题目内容
已知函数f(x)=[ln(a+x)]2+2ln(a+x)-2x,若x=0是函数f(x)的极值点,试证明:函数f(x)在(0,1)是减函数.
考点:利用导数研究函数的极值,函数单调性的判断与证明,利用导数研究函数的单调性
专题:证明题,函数的性质及应用,导数的综合应用
分析:求出函数f(x)的导数,x=0是函数f(x)的极值点,则f′(0)=0,通过g(x)=lnx-x+1的单调性和最值,可得a=1,再求f(x)的导数,运用g(x)的单调性,即可证得f(x)在(0,1)的导数小于0,进而得证.
解答:
证明:函数f(x)=[ln(a+x)]2+2ln(a+x)-2x的导数
f′(x)=2ln(a+x)•
+
-2,
x=0是函数f(x)的极值点,则f′(0)=0,
即有2lna•
+
-2=0,
即为lna-a+1=0,
令g(x)=lnx-x+1,
由(lnx-x+1)′=
-1,当x>1时,g′(x)<0,g(x)递减,
当0<x<1时,g′(x)>0,g(x)递增,
则有g(x)≤g(1),即为lnx-x+1≤0,
则lna-a+1=0,解得a=1,
则f(x)=[ln(1+x)]2+2ln(1+x)-2x的导数为
f′(x)=2ln(1+x)•
+
-2=
[ln(x+1)-(x+1)+1],
由0<x<1,则1<x+1<2,
则ln(x+1)-(x+1)+1<0,
即有f′(x)<0,
则函数f(x)在(0,1)是减函数.
f′(x)=2ln(a+x)•
| 1 |
| a+x |
| 2 |
| a+x |
x=0是函数f(x)的极值点,则f′(0)=0,
即有2lna•
| 1 |
| a |
| 2 |
| a |
即为lna-a+1=0,
令g(x)=lnx-x+1,
由(lnx-x+1)′=
| 1 |
| x |
当0<x<1时,g′(x)>0,g(x)递增,
则有g(x)≤g(1),即为lnx-x+1≤0,
则lna-a+1=0,解得a=1,
则f(x)=[ln(1+x)]2+2ln(1+x)-2x的导数为
f′(x)=2ln(1+x)•
| 1 |
| x+1 |
| 2 |
| x+1 |
| 2 |
| x+1 |
由0<x<1,则1<x+1<2,
则ln(x+1)-(x+1)+1<0,
即有f′(x)<0,
则函数f(x)在(0,1)是减函数.
点评:本题考查函数的极值与导数的关系,考查运用函数的导数证明函数的单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知向量
,
的模分别为1,2,它们的夹角为60°,则向量
-
与-4
+
的夹角为( )
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| A、60° | B、120° |
| C、30° | D、150° |
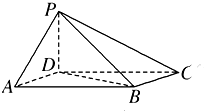 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2,AD=1,PD⊥底面ABCD.