题目内容
如果a>b,ab=1,求证:a2+b2≥2
(a-b)
| 2 |
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:利用ab=1,可得
=
=(a-b)+
,根据基本不等式,即可证明结论.
| a2+b2 |
| a-b |
| (a-b)2+2ab |
| a-b |
| 2 |
| a-b |
解答:
证明:∵ab=1,
∴
=
=(a-b)+
,
∵a>b,∴a-b>0
∴(a-b)+
≥2
,
当且仅当a-b=
时,取“=”
∴a2+b2≥2
(a-b).
∴
| a2+b2 |
| a-b |
| (a-b)2+2ab |
| a-b |
| 2 |
| a-b |
∵a>b,∴a-b>0
∴(a-b)+
| 2 |
| a-b |
| 2 |
当且仅当a-b=
| 2 |
| a-b |
∴a2+b2≥2
| 2 |
点评:本题考查不等式的证明,考查基本不等式的运用,正确变形是关键.

练习册系列答案
相关题目
若a>b>0,c>0,则下列各式错误的是( )
A、
| ||||
| B、a+c>b+c | ||||
| C、a-c<b-c | ||||
| D、ac>bc |
化简
可得( )
| log38 |
| log32 |
| A、log34 | ||
B、
| ||
| C、3 | ||
| D、4 |
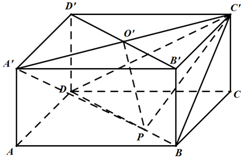 如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合).
如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合).