题目内容
已知向量
，
的模分别为1，2，它们的夹角为60°，则向量
-
与-4
+
的夹角为（ ）
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| A、60° | B、120° |
| C、30° | D、150° |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：利用向量
，
夹角公式cosθ=
，本题先求出
-
与-4
+
的模以及它们的数量积，再代入公式计算求解．
| a |
| b |
| ||||
|
|
| e1 |
| e2 |
| e1 |
| e2 |
解答：
解：∵（
-
）2=
2，-2
•
+
2=12-2×1×2×cos60°+22=3，
∴|
-
|=
，
同理求得（-4
+
）2=12，
|-4
+
|=2
．
又（
-
）•（-4
+
）=-4
2-3
•
+
2=-3，
利用向量
，
夹角公式cosθ=
．
得向量
-
与-4
+
的夹角为cosθ=
=-
，
∴θ=120°
故选B．
| e1 |
| e2 |
| e1 |
| e1 |
| e2 |
| e2 |
∴|
| e1 |
| e2 |
| 3 |
同理求得（-4
| e1 |
| e2 |
|-4
| e1 |
| e2 |
| 3 |
又（
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e1 |
| e2 |
| e2 |
利用向量
| a |
| b |
| ||||
|
|
得向量
| e1 |
| e2 |
| e1 |
| e2 |
| -3 | ||||
|
| 1 |
| 2 |
∴θ=120°
故选B．
点评：本题考查了向量夹角的计算，涉及到向量数量积德计算，模的计算知识比较基础，掌握基本的公式和技巧即可顺利求解
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
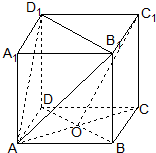已知正方体ABCD-A1B1C1D1，O是底面ABCD对角线的交点．不等式|x|＞3的解集为（ ）
| A、{x|x＞3} |
| B、{x|x＞±3} |
| C、{x|-3＜x＜3} |
| D、{x|x＜-3或x＞3} |